The inspiration for this post is…

1. Interview by Dr.Srinivasa Chakravarthy Head of Computation Neuroscience Lab at IIT, Madras and
2. Recent paper by Anirudh Goyal and Yoshua Bengio titled Inductive Biases for Deep Learning of Higher Level Cognition
3. Probabilistic Deep Learning with TensorFlow 2 course by Kevin Webster of Imperial College, London

I would be proud, if one finds this post is a commentary on Goyal and Benjio’s above mentioned paper inspired by Dr.Srinivas Chakravarthy’s approach towards understanding brain function.

Image Credit: Analytics India Mag

Objective

0. Prologue to Artificial General Intelligence
1. What is an inductive bias?
2. How human cognitive system used inductive biases?
3. What are the inductive biases used in deep learning?
4. What is Out-of-Distribution?
5. Simulation of Human like Intelligence using a Hypothesis space
6. Biologically inspired Deep Learning Architectures
7. What is Attention?
8. Overview to Interpretable Multi-Head Attention
9. Introduction to Multi-Horizon Forecasting using Temporal Fusion Transformers

Introduction

The beauty of deep learning systems is their inherent ability to learn and exploit the inductive biases from the train/validation dataset to achive certain level of convergence, that never yielded 100% accuracy. The in-distribution learning is the root cause for poor performance that lead to lack of generalization. Even for a simple linear equation $y = mx + c$ with clearly set prior knowledge, post training accuracy is not of appreciating level.
Reference: Finding Unknown Differentiable Equation - Automatic Differentiation Using Gradient Tapes

The key difference between the brain function and deep learning algorithms is the absence of backward pass(backpropagation) in the human cognitive system. I often ponder, Is evolution is nothing but a function of backpropagation happened for eons to bring us to wherever we are today in the form of humans(animals). I do not mind being called crazy and stupid to ask that question - I will be grateful, If I find an answer during my time over here part of my long journey.

Further, I believe human system is nothing but a bunch of sensors and actuators with a highly optimized PID controller called Brain for out-of-distribution scenarios to achieve generalization through transfer learning.

We Evolved Under Pressure

While great mammoths, neanderthals were going extinct, cockroaches and humans are thriving - facing similar challenges and threats reinforced the fact survival of the fittest. It happened due to the nature of that particular species for its ability to interact with multiple agents, newer environments, learn through competition and survive under constant pressure to achieve higher level of flexibility, robustness and adaptability.

Somewhere, we do not know how, where and when - human evolutionary process diverged from rest of the species to achieve systematic generalization through decomposition of knowledge into smaller pieces which can be recomposed dynamically to reason, imagine and create at an explicit level to achieve higher cognition.

Image Credit: Artificial Intelligence or the Evolution of Humanity

Beyond Data - Multiple Hypothesis and Hypothesis Space

Deep learning brought remarkable progress but needs to be extended in qualitative and not just quantitative 
ways(larger datasets and more computing resources).

Further says, 
having larger and more diverse datasets is important but insufficient without good architectural inductive 
biases.
- Goyal et al

At present we are quite successful and achieving good accuracy metrics for narrow tasks within boundaries under a context through

• Supervised learning where dataset is labeled or
• Reward and penalty based architectures like reinforcement learning

This is quite contrary and tangential to the nature of human learning system, the past knowledge - or the inductive priors of human cognitive system allows them to quickly generalize on new tasks and reuse previously acquired knowledge.

The dataset restricts the learner’s hypothesis space - It may be large enough for a context specific problem but quite small to ensure reliable generalization. Jonathan Baxter in his paper titled A Model of Inductive Bias Learning proposes a model and architectural scheme for bias learning. These models typically takes the following form…

A training dataset $z$ drawn independenty according to an underlying distribution $P$ on $\mathcal{X} \times \mathcal{Y}$ where $x_i \in \mathcal{X}$ and $y_i \in \mathcal{Y}$ spaces

$$z = {(x_1, y_1), \cdots, (x_m, y_m)}$$

Then the learning agent is supplied with a hypothesis space $\mathcal{H}$ Based on the information contained in $z$, the learning agent’s goal is to select a hypothesis $h: \mathcal{X} \rightarrow \mathcal{Y} $ by minimizing certain loss.

For example. this loss $er_P(h)$ could be a squared loss $$\large er_P(h):= \mathbf{E}_{(x, y)~P}(h(x) - y)^2$$

i.e. the empirical loss of $h$ on $z$ to be minimized is

$$\hat{er}_z(h) = \frac{1}{m} \sum_1^m l(h(x_i), y_i) \tag{1.Emperical Loss}$$

In such models the learner's bias is represented by the choice of H, if H does not contain a good solution 
to the problem, then, regardless of how much data the learner receives it cannot learn.
- Jonathan Baxter

Image Credit: Reaching for the gut of Machine Learning: A brief intro to CLT

The best way to model the inductive bias learning is to learn an environment of related learning tasks by supplying a family of hypothesis spaces $\mathcal{H} \in \mathbf{H}$ to the learning agent. Bias, that is learnt on such environments via sufficiently many training tasks is more likely to pave way for learning novel tasks belong to that environment.

for any sequence of $n$ hypothesis $(h_1, \cdots, h_n)$ the loss function is

$$(h_1, \cdots, h_n)_l ((x_1, y_1), \cdots, (x_m, y_m)) = \frac{1}{n} \sum_1^n \hat{er}_z(h_i) \tag{2. Overall Loss}$$

Even the approach presented above is quite a statistical learning framework with a twist by adding more hypothesis to the learning agent. This is still not sufficient for generalization unless we bring notions about learning agent and causality - even if the application is trying to classify cats and dog, the green pastures, sky and other stationary objects in the image should be part of the learning policy. This approach leads us not to think the data as set of examples drawn independently from the same distribution but reflect the real world.

General Purpose Learning

It is practically impossible to model a complete general-purpose learning system due to the fact they will implicitly or explicitly generalize better on certain distribution and fail on others. Is that why human beings are highly biased? Ain’t we all agree that the most sophisticated general purpose system is the human system.

The question for AI research aiming at human-level performance then is to 
identify inductive biases that are most relevant to the human perspective 
on the world around us.
- Goyal et al

What are Inductive Biases

We have a clarity that the past knowledge fed to the learning agent is all inductive bias is all about, following are the few concrete examples of inductive biases in deep learning

• Patterns of Features: Distributed representation of environment through various feature vectors
• Group Equivariance: The process of convolution over the 2D space
• Composistion of Functions: Deep architectures that perform various function to extract information
• Equivariance over Entities and Relations: Graph Neural Networks
• Equivariance over Time: Recurrent Networks
• Equivariance over Permutations: Soft Attention

These biases are encoded using various techniques like explicit regularisation objectives, having architectural constraints, parameter sharing, prior distribution in a Bayesian setup, convolution and pooling, data augmentation etc.
For example, in a transfer learning setup - With a strong inductive bias,

The first half of the training set already strongly contains what the learner should 
predict on the second half of the training set, which means that when we encounter these 
examples, their error is already low and training thus converges faster.
- Goyal et al

State of the art Deep Learning architectures for Object Detection and Natural Language Processing extracts information from past experiences and tasks to improve its learning speed. A significant level of generalization transferred to specific sample set of related task to the learner to give an idea

• What they have in common, what is stable and stationary across the environments experiences
• How they differ or how changes occur from one to the next in case we consider a sequential decision making scenarios

Out-of-Distribution Generalization

It is evident, generalization can be achieved only when we draw training observations outside of the specific distributions. The paper suggests OOD through sample complexity while facing new tasks or changing the distributions,

• 0-Shot OOD and
• k-Shot OOD

Achieving the sample complexity is studied in linguistics and the notion is called as systematic generalization. i.e. for a novel composition of existing concepts(e.g. words) can be derived systematically from the meaning of the composed concepts. Its nothing but comprehending a particular concept through various other factors which are not directly related to the concept of interest. For e.g. auditory lobe auguments the sound of a crow to classify the bird when it flies in the vicinity of the person.

This level of generalization makes it possible to decipher new combinations of zero probability under the training distribution. For e.g. creativity, innovation, new ideas etc or even science fiction. Emperical studies of such generalizations are performed by Bahdanau et al in the lingustics and nlp domain, with results no near comparable to human cognition.

Biological Inspiration - Attention

In this section, we shall explore the biological inspiration in deeplearning models. Focusing equivariance over permutation process of Attention. Attention is a concept from cognitive sciences, selective attention illustrates how we focus our attention to particular objects in the surroundings. This mechanism helps us to concentrate on things that are relevant and important and discard the unwanted information.

Image Credit: blog.floydhub.com

The most famous applications of Attention mechanism are

• Image Captioning: Based on the objects and their importance, the system generates a caption for the image
• Neural Machine Translation: Focus on the right few words to translate the left ones for English to French kind of translation.
• Multi Horizon Forecasting: It is similar to NMT, here the forecasting of next few values are done based on the historical sequence

Attention for Multi Horizon Forecasting of Temporal Data

An attention function can be described as mapping a query and set of key-value pairs to an output, 
where the query, keys, values and output are all vectors. The output is computed as a weighted 
sum of the values, where the weight assigned to each value is computed by a compatibility 
function of the query with the corresponding key.
- Vaswani et al, Attention is All You Need

Multi-horizon forecasting(MHF) often contains a complex mix of inputs - including static covariates, known future inputs and other exogenous time series that are only observed in the past - without any prior information on how they interact witht the target.

There are many DL architectures published for multi-horizon forecasting problems but most of them are black box models. In this section, we shall see Interpretable Multi Head Attention for Temporal Fusion Transformer(TFT). TFT is a novel attention based architecture which combines high performance multi-horizon forecasting with interpretable insights into temporal dynamics.

To learn temporal relationship at different scales, TFT uses Recurrent Neural Network(RNN) for local processing and interpretable self-attention layers for long-term dependencies. It utilizes specialized components to select relevant features and a series of gating layers to suppress unnecessary components, enabling high performance in a wide range of scenarios. The full details of TFT are beyond the scope of this article, we shall see the Interpretable Multi Head Attention in detail.

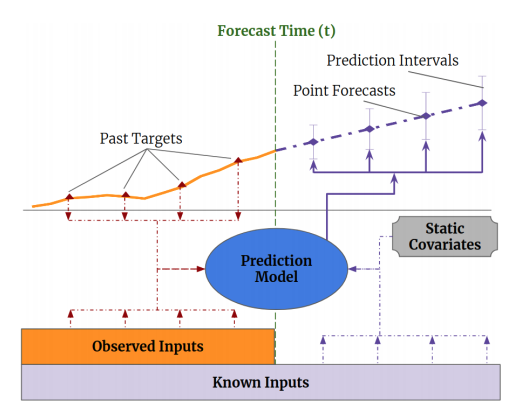
Image Credit: Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting

Interpretable Multi-Head Attention

TFT employs a self-attention mechanism to learn long-term relationships across different time steps, which we modify from multi-head attention in transformer based architectures[17, 12] to enhance explainability.

The Q, K and V

• Attention mechanisms scales values ${V} \in \mathbb{R}^{N \times d_v}$ relationship between keys(K) and queries(Q)
• $K \in \mathbb{R}^{N \times d_{attn}}$ is the Key
• $Q \in \mathbb{R}^{N \times d_{attn}}$ is the Query

$$Attention({Q, K, V}) = A({Q,K})V\tag{3}$$

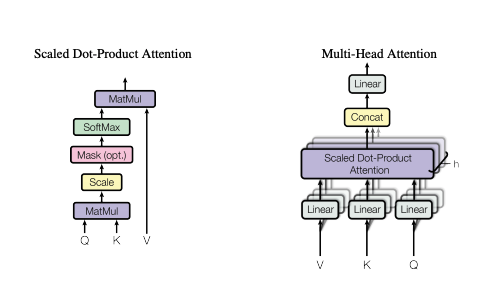
Image Credit: Attention is All You Need

Where,

• $A()$ is the normalization function - A common choice is scaled dot-product attention

$$A({Q,K}) = softmax \left(\frac{QK^T}{\sqrt{d_{attn}} } \right)\tag{4. Attention}$$

Multi Head Attention is proposed in employing different heads for different representation subspaces to increase the learning capacity $$MultiHead{(Q,K,V)}) = [H_1, \cdots, H_{m_H}]W_H\tag{5}$$ $$i.e.$$ $$H_h = Attention(QW^{(h)}_Q, KW^{(h)}_K, VW^{(h)}_V) \tag{6. Multi-Head Attention}$$

Where,

• $W_K^{(h)} \in \mathbb{R}^{d_{model} \times d_{attn}}$ is head specific weights for keys
• $W_Q^{(h)} \in \mathbb{R}^{d_{model} \times d_{attn}}$ is head specific weights for queries
• $W_V^{(h)} \in \mathbb{R}^{d_{model} \times d_{V}}$ is head specific weights for values

$W_H \in \mathbb{R}^{(m_h.d_V) \times d_{model}}$ linearly combines outputs contatenated from all heads $H_h$

1. Since different values are used in each head, attention weights alone is not indicative of a feature’s importance
2. Multi-head attention to share values in each head, and employ additive aggregation of all heads $$InterpretableMultiHead(Q, K, V) = \tilde H \tilde{W}_H \tag{7.Interpretable MH}$$ $\tilde H = \tilde A(Q, K)V W_V \tag{8}$

$$\tilde{H} = \huge { \normalsize \frac{1}{H} \sum_{h=1}^{m_H} A(QW_Q^{(h)}, KW_K^{(h)}) \huge }\normalsize VW_V \tag{9}$$
$$\tilde H = \frac{1}{H} \sum^{m_H}_{h=1} A(QW^{(h)}_Q, KW^{(h)}_K, VW_V)\tag{10}$$

Where,

• $W_v \in \mathbb{R}^{d_{model} \times d_V}$ are value weights shared across all heads
• $W_H \in \mathbb{R}^{d_{attn} \times d_{model}}$ is used for final linear mapping

1. Through this, each head can learn different temporal patterns, while attending to a common set of input features.
2. These features can be interpretted as a simple ensemble over attention weights into combined matrix $\tilde A(Q, K)$ Eq.8.
3. Compared to $A(Q, K)$ Eq.4 in $\tilde A(Q, K)$ Eq.8 yields an increased representation capacity in an efficient way

Inference

This post is quite abstract and a prologue to Artificial General Intelligence(AGI) with Out-of-Distribution as the focus area. It further discussed the inductive biases in current scheme of deep learning algorithms like transfer learning and mutiple hypothesis, hypothesis spaces. Further, It introduced Attention mechanism for time series forecasting. In the future posts, we shall discuss the inductive biases and out of distribution schemes in detail.

References

• A Model of Inductive Bias Learning by Jonathan Baxter - Journal of Artificial Intelligence Research
• Neural Machine Translation by Jointly Learning To Align and Translate by Bahdanau et al - ICLR 2015
• Attention is All You Need Vaswani et al - NIPS 2017
• Inductive Biases for Deep Learning of Higher-Level Cognition Goyal et al, 2021
• Soft & hard attention Jonathan Hui
• Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting by Pfister et al, 2020