Gowri Shankar

That Straight Line Looks a Bit Silly - Let Us Approximate A Sine Wave Using UAT

Posted November 29, 2021 by Gowri Shankar  ‐  4 min read

This is the continuation of my first post on the Universal Approximation Theorem. My previous post took a simple case of approximating a leading straight line and in this post, we are approximating a sinewave using numpy that is smoothed using a Gaussian Filter.

Please consider this article an annex for the previous post, I added a few anecdotes from various personalities to make it look a bit interesting. Please read my previous posts before reading this article for clarity. This post comes under the subtopic Convergence under Math for AI/ML section. Please refer to the previous posts here

Steps



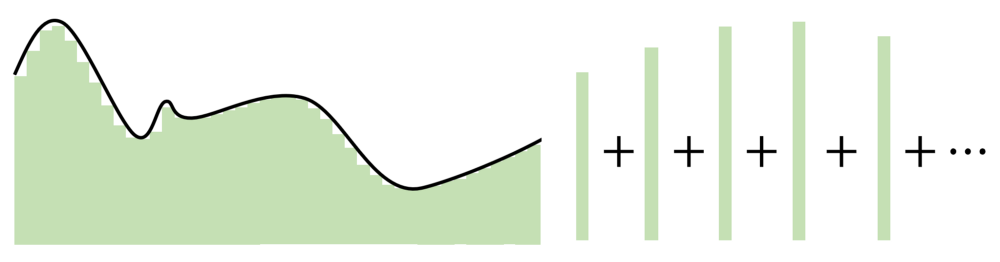
The key point in the Universal Approximation Theorem is that instead 
of creating complex mathematical relationships between the input and 
output, it uses simple linear manipulations to divvy up the complicated 
function into many small, less complicated pieces, each of which are 
taken by one neuron.

- Andre Ye

Objective

The objective of this article is to create a visual demonstration of approximating a sinewave in the 1-dimensional space.

Prologue

This post has 5 Sections that helps us to demonstrate the elegance of Universal Approximation Theorem by approximating a Sinewave

  • Single Neuron
  • Sine Wave Generator
  • Series of Step Functions
  • Tail Function

Single Neuron

Compare

Neurons

import numpy as np
import matplotlib.pyplot as plt

def neuron(inputt, weight, bias):
    f = lambda a, w, b: w * a + b
    step = lambda a, T: T if a >= T else 0

    f_of_x = f(inputt, weight, bias)
    output = [step(an_item, T) for an_item in f_of_x]

    return f_of_x, output

# Help functions to plot the graphs
def plot_steps(inputt, f_of_x, output, color, ax, title, label):
    ax.plot(inputt, f_of_x, color="green", label=f"f(x) = $\sum_i w_i x_i + bias$")
    ax.step(inputt, output, color=color, alpha=0.8, label=label)
    ax.set_title(title)
    ax.legend()
    ax.grid(True, which='both')
    ax.axhline(y=0, color='black', linewidth=4, linestyle="--")
    ax.axvline(x=0, color='black', linewidth=4, linestyle="--")

import matplotlib.image as mpimg
def render_image(ax, image_file):
    img = mpimg.imread(image_file)
    ax.imshow(img)

Sine Wave Generator



A sine wave is a geometric waveform that oscillates (moves up, down or 
side-to-side) periodically, and is defined by the function y = sin x. 
In other words, it is an s-shaped, smooth wave that oscillates above 
and below zero.

- Adam Hayes

Sinewave

# This code is written inspired by a stackoverflow post
# https://stackoverflow.com/questions/48043004/how-do-i-generate-a-sine-wave-using-python
from scipy.ndimage.filters import gaussian_filter1d

start_time = 0
end_time = 1
sample_rate = 10
time = np.arange(0, 10, 1)
theta = 0
frequency = 100
amplitude = 1
sinewave = amplitude * np.sin(2 * np.pi * frequency * time + theta) / 1e-14
_, axes = plt.subplots(1, 2, figsize=(20, 6), dpi=80)
axes[0].plot(sinewave, label="Sinewave")
smooth_sine = gaussian_filter1d(sinewave, sigma=2)
smooth_sine = np.array([round(item) + 10 for item in smooth_sine])
axes[1].plot(smooth_sine, label="Smoothened Sinewave")
plt.legend()
axes[0].grid(True, which='both')
axes[0].axhline(y=0, color='black', linewidth=4, linestyle="--")
axes[0].axvline(x=0, color='black', linewidth=4, linestyle="--")
axes[1].grid(True, which='both')
axes[1].axhline(y=0, color='black', linewidth=4, linestyle="--")
axes[1].axvline(x=0, color='black', linewidth=4, linestyle="--")

<matplotlib.lines.Line2D at 0x7f8adaf47970>

png

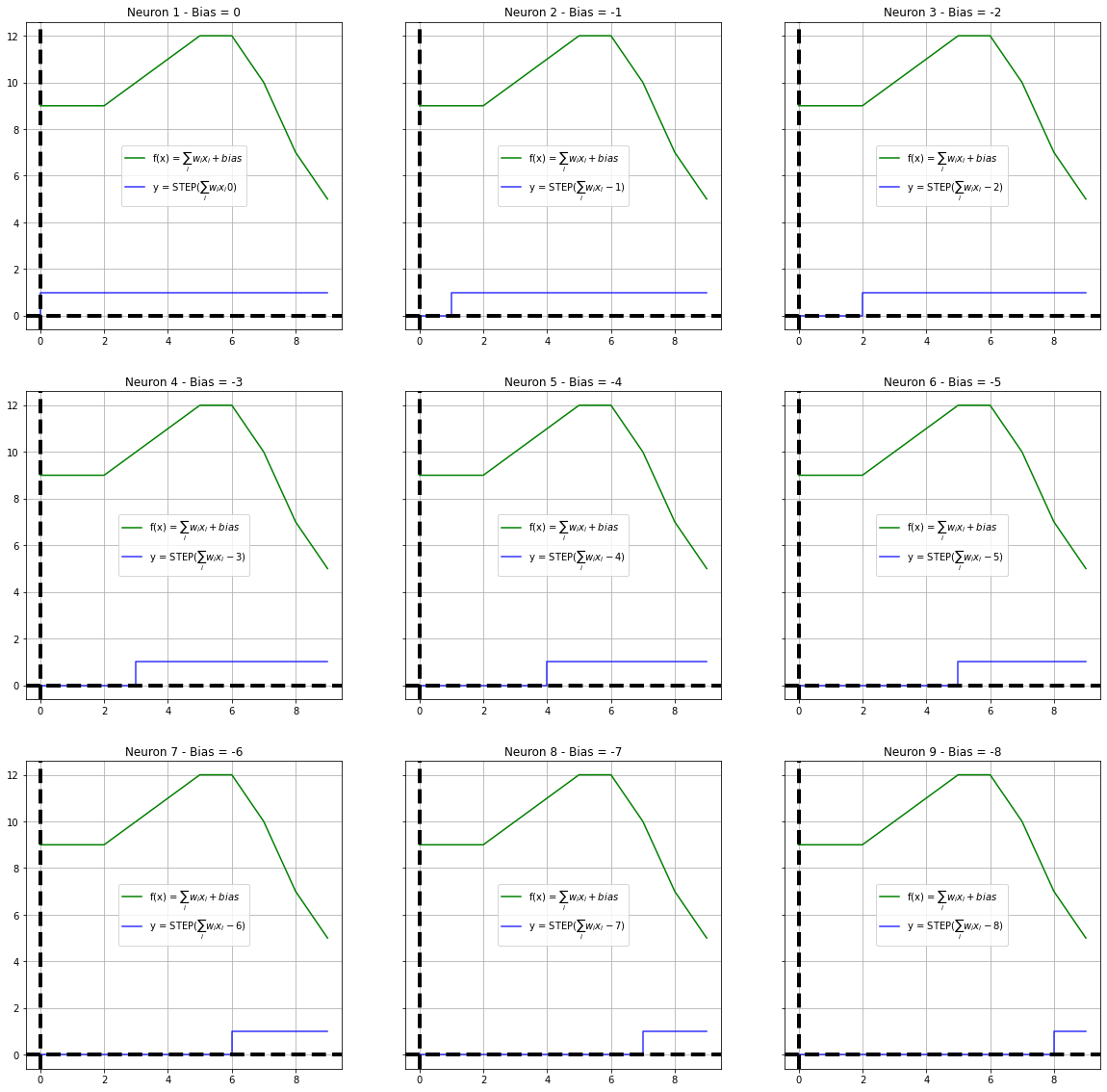
Simulating Series of Steps

We are creating 9 neurons in the the hidden layer and approximating the sinewave.

x = np.arange(10)
w = 1
T = 1
y = smooth_sine
fig, axes = plt.subplots(3, 3, figsize=(20, 20), sharey=True)
bias = -x
col = 0
row = 0
steps = []
for idx in np.arange(10):
    b = bias[idx]

    if col == 3:
        row += 1
        col = 0


    _, gx = neuron(x, w, b)
    steps.append(gx)
    if((col != 3) and (row != 3)):
        plot_steps(x, y, steps[idx], "blue", axes[row, col], f"Neuron {idx + 1} - Bias = {b}", label=f"y = STEP($\sum_i w_i x_i {b}$)")
    col += 1

png

Tail Function

fig, axes = plt.subplots(3, 3, figsize=(20, 20), sharey=True)
bias = -x
print (axes.shape, x, bias)
col = 0
row = 0
tails = []
for idx in np.arange(9):
    b = bias[idx]
    tail = list(y[idx] * (np.array(steps[idx]) - np.array(steps[idx + 1])))
    tails.append(np.array(list(y[idx] * (np.array(steps[idx]) - np.array(steps[idx + 1])))))

    if col == 3:
        row += 1
        col = 0
    plot_steps(x, y, tail, "blue", axes[row, col], f"Neuron 1 - Bias = {b}", label=f"y = STEP($\sum_i w_i x_i {b}$)")
    col += 1

(3, 3) [0 1 2 3 4 5 6 7 8 9] [ 0 -1 -2 -3 -4 -5 -6 -7 -8 -9]

png

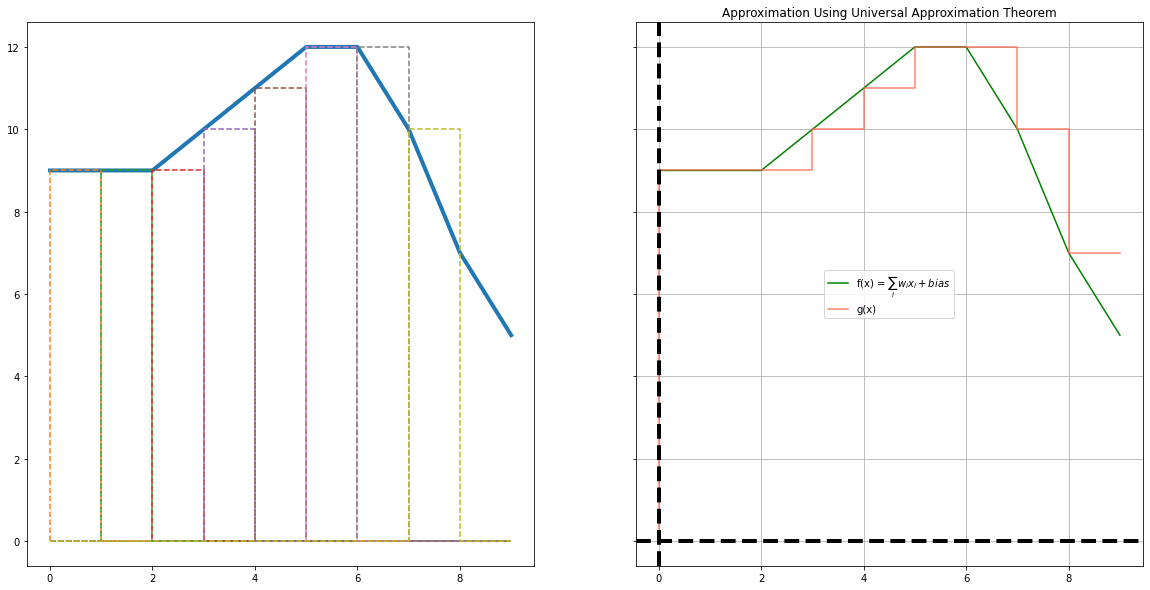
fig, axes = plt.subplots(1, 2, figsize=(20, 10), sharey=True)
bias = -x
axes[0].plot(x, y,linewidth=4)
for idx in np.arange(8):

    axes[0].step(x, tails[idx], linestyle="--")
gx = np.sum(tails, axis=0)
plot_steps(x, y, gx, "tomato", axes[1], title="Sum of Steps", label="g(x)")
plt.title("Approximation Using Universal Approximation Theorem")

Text(0.5, 1.0, 'Approximation Using Universal Approximation Theorem')

png

Epilogue

This is a continuation of the previous article on UAT inspired by Layra Ruis’ review on the paper Learning in High Dimension Always Amounts to Extrapolation. In this post, we approximated a sinusoidal wave using a neural network with 1 hidden layer. I am glad to present this topic, I had a few new learnings and hope my readers too. I thank everyone who inspired me to write this post, It is an amazing experience.

References