In this post, we shall study the mathematical intuition behind DCNs. Then we shall build one using a relatively new library called TensorFlow Recommenders(TFRS) for building Deep Learning Recommendation Models(DLRM). This post comes under a new subtopic Recommenders of the section AI/ML. Please refer to the past posts under the section AI/ML here,

• Post on Machine Learning and Artificial Intelligence

We aim to avoid task-specific feature engineering
by introducing a novel neural network structure – a cross network
– that explicitly applies feature crossing in an automatic fashion.
The cross network consists of multiple layers, where the highest 
degree of interactions are provably determined by layer depth. Each
layer produces higher-order interactions based on existing ones,
and keeps the interactions from previous layers. We train the cross
network jointly with a deep neural network

- Wang, Fu et al
 

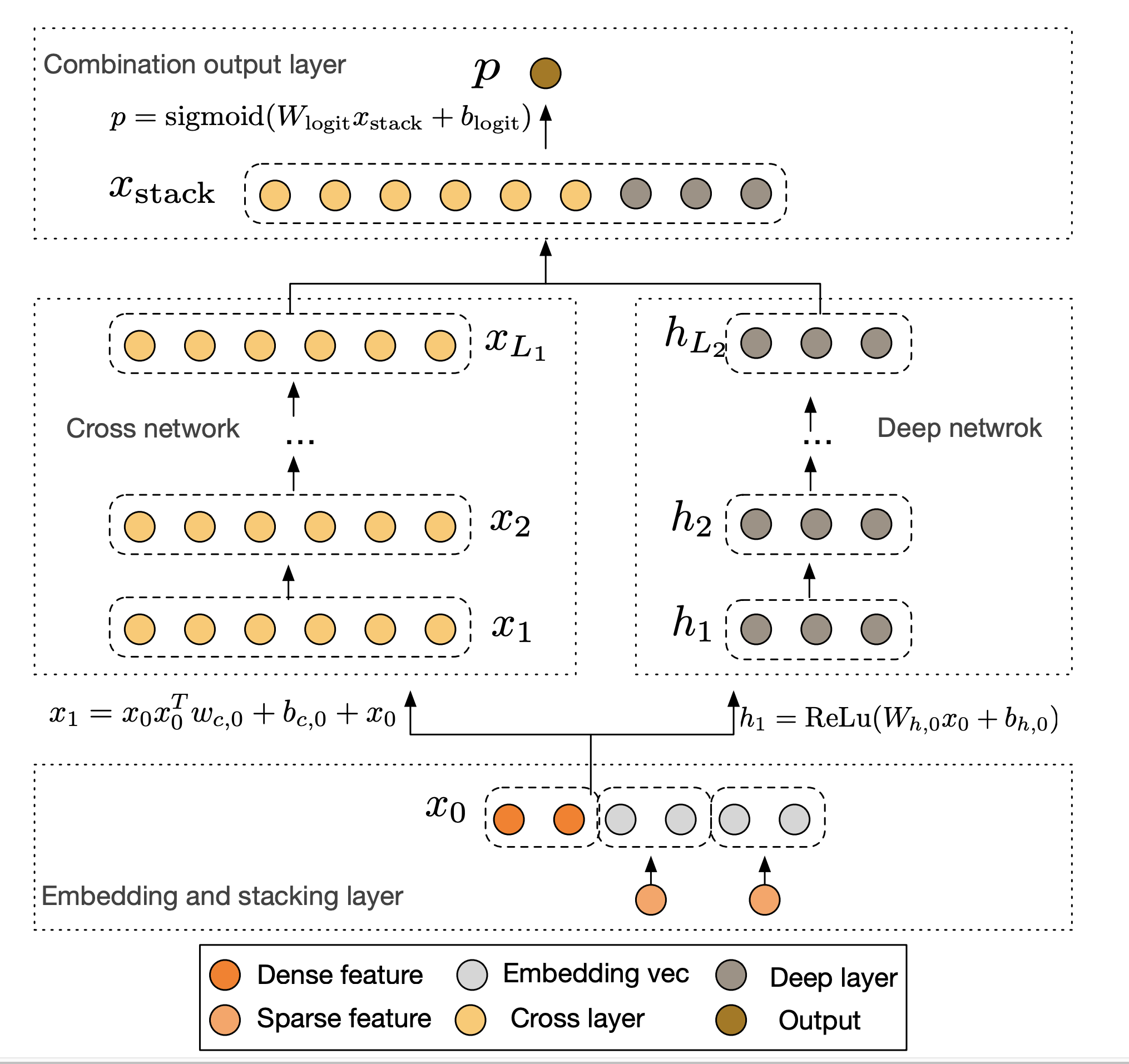
This post is a walk-through of the paper titled Deep & Cross Network for Ad Click Predictions by Wang, Fu et al from Stanford University and Google. I thank Khalid Salama for writing a detailed description of deep and cross networks under the title Structured data learning with Wide, Deep, and Cross networks in Keras tutorial. I tried to reproduce his work with my creativity and curiosity.

The below implementation is influenced by the original post from the TensorFlow tutorial

Objective

The objective of this post is to understand the need for Deep and Cross Networks(DCN), their mathematical background, and implement a simple DCN using synthetic data. In that process, we shall learn the functional APIs of the TensorFlow Recommenders package for model construction and ranking.

Introduction

Feature engineering is often done manually and it is an extensive task that does not scale for larger dimensional datasets. E.g. It is a near-impossible task to build a recommendation model for a Consumer Packaging Goods(CPG) manufacturer with more than a million retail stores selling 1000s of products under various categories. Here the number of shops to cater to is the dimensionality of the sales dataset. Similarly, we can find higher-dimensional datasets in the finance and banking industry also in an OTT platform. Often, the recommendation models of the past are linear(logistic) in nature and the natural evolution was Factorization Machines(FMs) and subsequently Field-aware Factorization Machines(FFMs) with their shortcomings and pitfalls.

• Image Credit: An Intuitive Explanation of Field Aware Factorization Machines

With the invention of Embeddings where the features are encoded into low-dimensional dense vectors, the learnability of the overall model remarkably increases, using Wide and Deep Networks. Our systems are evolved now to cross the features to bring in the highly nonlinear effective representation of interactions.

Deep and Cross Network(DCN)

The need for DCN arises for 2 reasons. First, automatic feature learning with both sparse and dense inputs without any manual effort or exhaustive search. Second, a scale for millions of parameters in a typical enterprise-level application recommendation needs.

The cross network is simple yet effective. By design, the highest
polynomial degree increases at each layer and is determined by
layer depth. The network consists of all the cross terms of degree
up to the highest, with their coefficients all different.

- Wang, Fu et al
 

DCN Building Blocks

A DCN Network is constructed using 4 building blocks,

1. Embedding and Stacking Layer
2. Cross Network
3. Deep Network
4. Combination Layer

We shall study them all in the subsequent sections.

Embedding Layer

In most of the use cases, the variables are categorical - for example user ids, country names, product brand, etc. They are often represented in high-dimensional features space with a larger memory footprint. We call those values of the variables as a vocabulary of the feature element. Using embeddings, the dimensionality of the feature space can be reduced by turning them into dense vectors of real values as follows,

$$\Large x_{embed, i} = W_{embed, i} x_i \tag{1. Embedding Vectors}$$

Where,

• $x_i$ is the binary input in the $i^{th}$ category
• $W_{embed, i} \in \mathbb{R}^{n_e \times n_v}$ is the embedding matrix
• $n_e$ is the embedding size and
• $n_v$ is the vocabulary size

The Embedding vectors are stacked along with the normalized dense features as follows, $$\Large x_0 = \left[x_{embed, 1}^T, x_{embed, 2}^T, \cdots, x_{embed, k}^T, x_{dense}^T \right] \tag{2. Stacked Embedding Vectors}$$

Where $x_{dense}$ is the normalized dense features.

Cross Network

Let us say a student in his early 20s making an online purchase of a pocket-friendly dark rum bottle and a can of soda, what are the odds that he will buy an expensive pack of roasted almonds? Here we brought in 5 unique features,

1. Age of buyer
2. His current employability status
3. Purchasing a product - A bottle of dark rum
4. Purchasing a product - A can of soda
5. Purchasing a product - A pack of roasted almonds

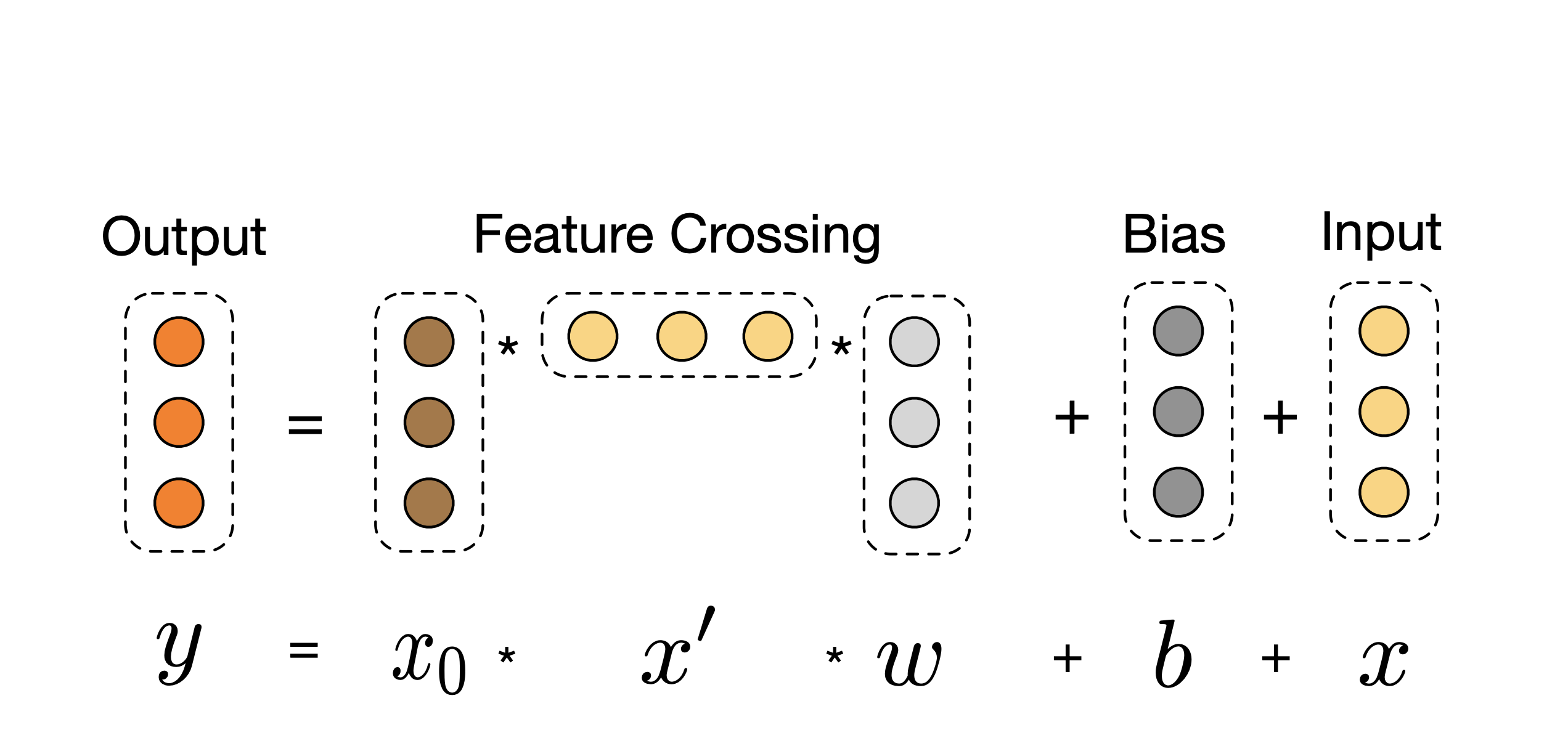
• Image Credit: Deep & Cross Network for Ad Click Predictions

The objective of this problem is to recommend the buyer to buy a pack of roasted almonds in the form of an advertisement or not. Subsequently, if we recommend what is the probability that that there will be a sale of roasted almonds. The combination of dark rum and a can of soda with the employability status of the buyer is called feature crosses.

When we design the DNN for feature crosses, we ensure each layer has the following composition of things, $$\Large x_{l + 1} = x_0 x_l^T w_l + b_l + x_l = f(x_l, w_l, b_l) + x_l \tag{3. Feature Cross Layer}$$

Where,

• $x_l, x_{l+1} \in \mathbb{R}^d$ are column vectors denoting the outputs from the $l^{th}$ and $(l+1)^{th}$ cross layers
• $w_l, b_l \in \mathbb{R}^d$ are the weight and bias of the $l^{th}$ layer
• Each cross layer adds back its input after a feature crossing $f$ and the mapping function $f: \mathbb{R}^d \mapsto \mathbb{R}^d$ fits the residual of $x_{l+1} - x_l$

The special structure of the cross-network causes the degree of cross features to grow with layer depth - Wang et al

Weierstrass Approximation Theorem

According to Weierstraas Approximation Theorem, any function under a certain smoothness assumption can be approximated by a polynomial to an arbitrary accuracy. The cross-network approximates the polynomial class of the same degree in a way that is efficient, expressive, and generalizes better to real-world datasets.

Let $P_n(x)$ be the multivariate polynomial class of degree n,

$$P_n(x) = { \sum_{\alpha} w_{\alpha} x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_d^{\alpha_d} | 0 \leq |\alpha| \leq n, \alpha \in \mathbb{N}^d } \tag{4. Multivariate Polynomial Class}$$ Where,

• $\alpha$ is the degree of a cross term defined as $x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_d^{\alpha_d}$ - where the degree of a polynomial is defined by the highest degree of its terms. The degree of cross features to grow with layer depth

• The $i^{th}$ element in $w_j$ be $w_j^{(i)}$, for a multi-index $\alpha = [\alpha_1, \alpha_2, \cdots, \alpha_d] \in \mathbb{N}^d$ and $x = [x_1, x_2, \cdots, x_d] \in \mathbb{R}^d$, we define $\alpha$ as
  $$|\alpha| = \sum_{i=1}^d \alpha_i \tag{5. Degree of the Cross Term}$$

Each polynomial in this class hasO(d^n) coefficients. We show that,
with onlyO(d) parameters, the cross network contains all the cross
terms occurring in the polynomial of the same degree, with each
term’s coefficient distinct from each other.

- Wang, Fu et al
 

Deep Network

The deep network is the conventional fully connected feed forward layer layer as follows $$h_{l+1} = f(W_lh_l + b_l) \tag{6. Deep Network FF Layer}$$ Where,

• $h_l \in \mathbb{R}^{n_l}, h_{l+1} \in \mathbb{R}^{n_{l + 1}}$ are the $l^{th}$ and $(l+1)^{th}$ hidden layers respectively
• $W_l \in \mathbb{R}^{n_{l+1} \times n_l}, b_l \in \mathbb{R}^{n_{l+1}}$ are the weights and the biases respectively
• $f(.)$ is the activation function

Combination Layer

The combination layer concatenates the cross and deep netowork outputs as follows, $$p = \sigma \left([x_{L_1}^T, h_{L_2}^T]w_{logits} \right) \tag{7. Combination Layer of 2-Class Classification}$$

Where,

• $x_{L_1} \in \mathbb{R}^d$ is the output from deep network
• $ h_{L_2} \in \mathbb{R}^m$ is the output from deep network
• $\sigma$ is the sigmoid activation function.

Loss Function

Loss function is the log-loss fucntion with a regularization term, $$loss = - \frac{1}{N} \sum_{i=1}^N y_i log(p_i) + (1 - y_i)log(1-p_i) + \lambda \sum_l ||w_l||^2 \tag{8. Log-Loss Function}$$ Where,

• $p_i$ is the probabilities computed from $eqn.7$
• $y_i$ is the label to be classified as
• $N$ is the total number of inputs
• $\lambda$ is the $L_2$ regularization parameter

Deep Cross Networks - Implementation

This section was significantly inspired by the tutorial for DCN from the TensorFlow Recommenders page. Refer here

We shall simulate a condition of the student buying alcohol and a can of soda

1. Age of buyer$(x_1)$ - $[18 - 80]$
2. His current employability status$(x_2)$ - $[0, 1]$
3. Purchasing a product - A bottle of dark rum$(x_3)$ - $[1, 0]$
4. Purchasing a product - A can of soda$(x_4)$ - $[0, 1]$
5. Purchasing a product - A pack of roasted almonds$(x_5)$ - $[0, 1]$
6. The likelihood of clicking an almond ad $y$

$$\Large y = f(x_1, x_2, x_3, x_4, x_5) = 0.1 x_1 + 1.2 x_2 + 0.5 x_3 + 0.2 x_4 + 1.8 x_2 x_3 + 0.1 x_2 x_4 + 3.1 x_2 x_5 + 1.5 x_3 x_5 + 2 x_2 x_3 x_4 x_5$$

The weight coefficients convey there is the chances of buying an almond pack is depend on the employability status. i.e I have given more weightage for employability status wherever it occurs.

Generate Synthetic Data

Let us generate a synthetic data based on the above equation using numpy random APIs.

import numpy as np
def generate_synthetic_data(num_observations=100_000, random_seed=42):
    rng = np.random.RandomState(random_seed)
    age = rng.randint(18, 80, size=[num_observations, 1]) / (80 - 12)
    employed = rng.randint(2, size=[num_observations, 1]) / 2
    rum = rng.randint(2, size=[num_observations, 1]) / 2
    soda = rng.randint(2, size=[num_observations, 1]) / 2
    almond = rng.randint(2, size=[num_observations, 1]) / 2

    x = np.concatenate([age, employed, rum, soda, almond], axis=1)

    y = 0.1 * age + 1.2 * employed + 0.5 * rum + 0.2 * soda +  1.8 * employed * rum + 0.1 * employed * soda + 3.1 * employed * almond + 1.5 * rum * almond + 2 * employed * rum * soda * almond

    return x, y

x, y = generate_synthetic_data()

num_train = 70000
train_x = x[:num_train]
train_y = y[:num_train]
eval_x = x[num_train:]
eval_y = y[num_train:]

TFRS Model Construction

TFRS helps us build recommender models simply and intuitively. We use tfrs.Model class, which encapsulates most of the challenges in building recommender models at scale. Further, we are using ranking tasks from TFRS tfrs.tasks.Ranking. Ranking

Recommender systems are often composed of two components:

- a retrieval model, retrieving O(thousands) candidates 
    from a corpus of O(millions) candidates.
- a ranker model, scoring the candidates retrieved by the 
    retrieval model to return a ranked shortlist of a 
    few dozen candidates.
This task helps with building ranker models. Usually, these 
will involve predicting signals such as clicks, cart 
additions, likes, ratings, and purchases.

- TensorFlow Recommenders
 

import tensorflow as tf
import tensorflow_recommenders as tfrs
class Model(tfrs.Model):

    def __init__(self, model):
        super().__init__()
        self._model = model
        self._logit_layer = tf.keras.layers.Dense(1)

        self.task = tfrs.tasks.Ranking(
          loss=tf.keras.losses.MeanSquaredError(),
          metrics=[
            tf.keras.metrics.RootMeanSquaredError("RMSE")
          ]
        )

    def call(self, x):
        x = self._model(x)
        return self._logit_layer(x)

    def compute_loss(self, features, training=False):
        x, labels = features
        scores = self(x)

        return self.task(
            labels=labels,
            predictions=scores,
        )

crossnet = Model(tfrs.layers.dcn.Cross())
deepnet = Model(
    tf.keras.Sequential([
      tf.keras.layers.Dense(512, activation="relu"),
      tf.keras.layers.Dense(256, activation="relu"),
      tf.keras.layers.Dense(128, activation="relu")
    ])
)

2021-12-10 17:21:01.662851: I tensorflow/core/platform/cpu_feature_guard.cc:151] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations:  AVX2 FMA
To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags.

train_data = tf.data.Dataset.from_tensor_slices((train_x, train_y)).batch(1000)
eval_data = tf.data.Dataset.from_tensor_slices((eval_x, eval_y)).batch(1000)

epochs = 100
learning_rate = 0.4
crossnet.compile(optimizer=tf.keras.optimizers.Adam(learning_rate))
crossnet.fit(train_data, epochs=epochs, verbose=False)
deepnet.compile(optimizer=tf.keras.optimizers.Adam(learning_rate))
deepnet.fit(train_data, epochs=epochs, verbose=False)

<keras.callbacks.History at 0x7fc9735a55e0>

crossnet_result = crossnet.evaluate(eval_data, return_dict=True, verbose=False)
print(f"CrossNet(1 layer) RMSE is {crossnet_result['RMSE']:.4f} "
      f"using {crossnet.count_params()} parameters.")

deepnet_result = deepnet.evaluate(eval_data, return_dict=True, verbose=False)
print(f"DeepNet(large) RMSE is {deepnet_result['RMSE']:.4f} "
      f"using {deepnet.count_params()} parameters.")

CrossNet(1 layer) RMSE is 0.0281 using 36 parameters.
DeepNet(large) RMSE is 0.8087 using 167425 parameters.

Model Understanding

Our goal is to learn the feature crosses and identify the most statistically significant feature interactions. This can be verified by observing the learned weight matrix in DCN.

import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable

mat = crossnet._model._dense.kernel
features = ["age", "employed", "rum", "soda", "almonds"]

plt.figure(figsize=(10,10))
im = plt.imshow(np.abs(mat.numpy()), cmap=plt.cm.Blues)
ax = plt.gca()
ax.tick_params(labelsize=10)
_ = ax.set_xticklabels([''] + features, rotation=45, fontsize=10)
_ = ax.set_yticklabels([''] + features, fontsize=10)

/var/folders/wh/h43cl57j4ljf1x5_4p1bqmx80000gn/T/ipykernel_4160/3080520049.py:11: UserWarning: FixedFormatter should only be used together with FixedLocator
  _ = ax.set_xticklabels([''] + features, rotation=45, fontsize=10)
/var/folders/wh/h43cl57j4ljf1x5_4p1bqmx80000gn/T/ipykernel_4160/3080520049.py:12: UserWarning: FixedFormatter should only be used together with FixedLocator
  _ = ax.set_yticklabels([''] + features, fontsize=10)

Epilogue

It is quite convincingly proved the interaction between being employed has significance in buying expensive almonds from the online store. This post is a walk-through of Wang et al’s paper titled Deep & Cross Network for Ad Click Predictions, We studied the significance of feature crossing, mathematical intuition behind feature crossing, and finally generated synthetic data to prove the same. Our goal was to understand the architecture of DCNs and demonstrate how it works.

tfrs-for-dlrms-at-enterprise-scale-a-practical-guide-to-Understand-deep-and-cross-networks