We studied Dequantization process from a different context in the past where we have learned how to approach categorical values in a probabilistic setup. In this post, we shall study the mathematical intuition behind the embedding process and a novel method of embedding that is memory efficient. Please refer to the previous posts on this topic here,

• Dequantization for Categorical Data, Categorical NFs via Continuous Transformations - A Paper Review

This post comes under the sub-topic Fundamentals of ML/AI, previously published articles can be referred here

• Image Credit: Travel Mode Choice Prediction Using Deep Neural Networks With Entity Embeddings

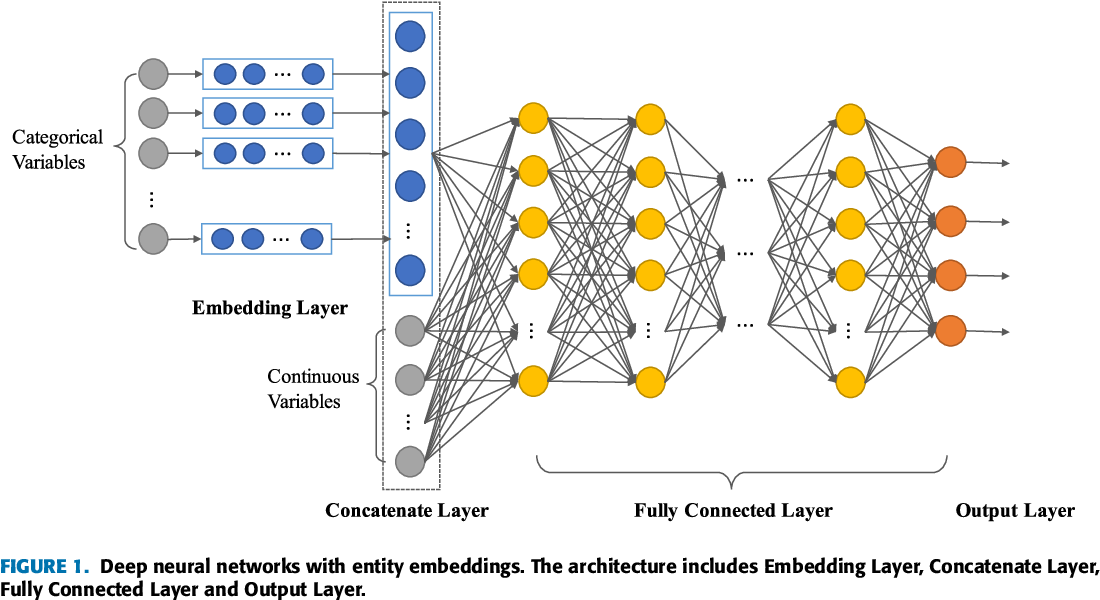
When you instantiate an Embedding layer, its weights (its internal dictionary
of token vectors) are initially random, just as with any other layer. During 
training, these word vectors are gradually adjusted via backpropagation, 
structuring the space into something the downstream model can exploit. Once 
fully trained, the embedding space will show a lot of structure—a kind of 
structure specialized for the specific problem for which you’re training 
your model.

- Deep Learning with Python by F. Chollet

This post is a review of the paper titled Compositional Embeddings Using Complementary Partitions for Memory-Efficient Recommendation Systems by Shi, Naumov et al of Facebook. I thank Khalid Salama for writing a guide to understand the QR embedding technique here

Objective

The objective of this post is to learn how to work with categorical variables for a deep learning model. In that quest, we shall explore a novel approach called Quotient-Remainder Trick for Embedding and its significance.

Prologue

We collect and store categorical data from almost all the quarters of the software systems. User details and identification information, Product categories, brands, and shop information in retail systems, Countries, states, and cities in a geographical information system, etc are a few of the categorical values that are commonly observed while developing a deep learning model of a structured data set. Efficiently making use of them is not anything trivial, i.e we are in the quest of transforming the discrete entities defined for the convenience of storage and retrieval to continuous signals that transform one form to another in a progressive manner. A concrete example will make the intuition behind the transformation easier to comprehend. Let us take two retail outlets in the same geography physically displaced by a few meters, the first shop is a mom-and-pop store and the second one is a supermarket. The small shop’s owner would aspire to grow his sales to the scale of the nearby supermarket. Let us consider the data that we have collected represent the shops as

{
    "mom and pop": 0, 
    "small store": 1, 
    "large store": 2, 
    "supermarket": 3
}

How this transition can happen from a mom and pop store to a supermarket? From the data given above, it looks like the natural transition mechanism would be of the following kind,

$$\Large mom \ and \ pop \rightarrow small \ store \rightarrow large \ store \rightarrow supermarket$$

However, this scheme is quite representational in the discrete space. There must be a chance of multiple(if not infinite in practice) transitions when the transition of ${0 \rightarrow 1 }$ occurs, making it evident that there are manifolds of infinite possibilities. i.e Our models are expected to learn a lot of things in the continuous space. Hence we transform the categorical values into embedding maps in a dense representational form.

import tensorflow as tf
import numpy as np

shop_categories = {
    "mom and pop": 0,
    "small store": 1,
    "large store": 2,
    "supermarket": 3
}
category_count = len(np.unique(list(shop_categories.values())))
category_count

4

The Embedding Layer

The classic definition for an embedding layer is it is a dictionary that maps the integer indices to a dense vector. In the following example, we shall demonstrate the embedding layer by,

1. Creating a simple Sequential model with an Embedding layer
2. Specify the category_count as the input dimension and several choices for the output dimension
3. Create random integer within the boundary of the category count and simulate its dense representation

NUM_EMBED_DIM = 5
def create_embedding_model(embed_layer):
    model = tf.keras.models.Sequential()
    model.add(embed_layer)
    model.compile("rmsprop", "mse")
    return model

embed_layer = tf.keras.layers.Embedding(category_count, NUM_EMBED_DIM)
simple_model = create_embedding_model(embed_layer)

inputt = np.random.randint(category_count, size=(1, 1))
output = simple_model.predict(inputt)
print(f"Embeddings for the values {inputt} as dense representation: \n{output}")

Embeddings for the values [[1]] as dense representation:
[[[-0.03618066  0.03691795  0.03859289 -0.01019295  0.02414801]]]

The input data is of the format $[batch_size, input_length]$

inputt = np.random.randint(category_count, size=(1, 2))
output = simple_model.predict(inputt)
print(f"Embeddings for the values {inputt} as dense representation: \n{output}")

Embeddings for the values [[2 0]] as dense representation:
[[[-0.01420986 -0.01162178  0.04746081 -0.01824342 -0.0288559 ]
  [-0.01345457 -0.00952753  0.0035112   0.00534022 -0.02052623]]]

We had 1 batch and 2 inputs, a unique dense representation in an embedded space for each input. i.e For a set of categories $S, |S| = 4$ in our shop categories example. Each category is mapped to an indexed vector in the embedding table.

$$ W \in \mathbb{R}^{|S| \times D} \tag{1. Embedding Weight}$$

Our deep learning models are going to learn these weights during the training time along with the weights and biases of the rest of the neural networks.

Let us take the case of user identification or the number of retail outlets of a consumer package goods industry. We have a billion consumers catered by millions of shops, and they are identified as categorical values. What would be the storage complexity of the factor $|S| \times D \rightarrow O(|S|D)$ - By the way, we need a large embedding dimension($D$) to uniquely represent the shops and users.

If we reduce the embedding dimension $D$

different categories end up with the same embedding vector, resulting 
in loss of information and deterioration in model quality 

- Shi et al

Naive Approach to Reduce Embedding Table

Let us say $\epsilon$ is a single category with it’s index $i$ where $\epsilon : S \rightarrow {0, \cdots, |S| - 1}$. Then we can encode each category with index $i = \epsilon(x)$ with a 1-hot vector by $e_i \in \mathbb{R}^D$, then $$x_{emb} = W^T e_i$$ Where, $x_{emb} \in \mathbb{R}^D$ is the dense embedding vector. This whole setup yields a memory complexity of $O(|S|D)$. This

The naive approach of reducing the embedding table is to use a
simple hash function, such as the remainder function, called
the hashing trick.

- Shi et al

Let us fetch a smaller embedding table($\tilde{W} \in \mathbb{R}^{m \times D}$), where $m \ll S$ - one can define a hash matrix $R \in \mathbb{R}^{m \times |S|}$ $$R_{i, j} = \Large{ \normalsize \begin{array}{rcl} \text{1 if j mod m = i} \ \text{0 otherwise} \end{array} }$$ then the embedding is performed by

$$x_{emb} = \tilde{\mathbf{W}}^T R e_i$$

This naive approach is also weak in nature because $m \ll S$ result in loss of information and model deterioration.

Quotient-Remainder Trick(QR Trick)

QR Trick assumes $m$ is a factor of $|S|$ results in an integer quotient - using two complementary functions, the integer quotient and remainder function we can produce two separate embedding tables and combine the embeddings in such a way that a unique embedding is produced.

Two embedding tables $W_1 \in \mathbb{R}^{m \times D}$ and $W_2 \in \mathbb{R}^{(\frac{|S|}{m} \times D)}$
STEP 1: Determine $i = \epsilon(x)$ of category $x$
STEP 2: Compute hash indices $j = i \ MOD \ m$ and $k = \frac{i}{m}$
STEP 3: Look up embeddings $x_{rem} = (W_1)j$
STEP 4: Look up $x{quo} = (W_2)k$
STEP 5: Compute $x{emb} = x_{rem} \odot x_{quo}$

$$i.e.$$ $$Q_{i, j} = \Large { \normalsize \begin{array}{rcl} \text{1 if j // m = i} \ \text{0 otherwise} \end{array} }$$ $$then$$ $$x_{emb} = W_1^T R e_i \odot W_2^T Q e_i$$

Below implementation of QR Trick is inspired by Khalid Salama’s code from keras tutorial

vocab = np.unique(list(shop_categories.keys()))
vocab = tf.convert_to_tensor(
    vocab, dtype=None, dtype_hint=None, name=None
)
index_lookup = tf.keras.layers.StringLookup(
    vocabulary=vocab, mask_token=None, num_oov_indices=0
)
q_embeddings = tf.keras.layers.Embedding(category_count, NUM_EMBED_DIM,)
r_embeddings = tf.keras.layers.Embedding(category_count, NUM_EMBED_DIM,)

embedding_index = index_lookup("supermarket")
quotient_index = tf.math.floordiv(embedding_index, 1)
remainder_index = tf.math.floormod(embedding_index, 1)
remainder_embedding = r_embeddings(remainder_index)
quotient_embedding = q_embeddings(quotient_index)

embedding_index, quotient_index, remainder_index

(<tf.Tensor: shape=(), dtype=int64, numpy=3>,
 <tf.Tensor: shape=(), dtype=int64, numpy=3>,
 <tf.Tensor: shape=(), dtype=int64, numpy=0>)

quotient_embedding * remainder_embedding

<tf.Tensor: shape=(5,), dtype=float32, numpy=
array([ 5.1096542e-04, -4.6359975e-04, -8.2595140e-04,  4.8001795e-05,
       -1.0725884e-03], dtype=float32)>

Epilogue

In this post, we studied the basics of the embedding technique and its utility in transforming categorical data from discrete space to continuous space. An Embedding layer behaves similar to a Dense layer where a weight matrix is a look-up dictionary. The key difference between a Dense layer and an Embedding layer is there are no activation functions that lead to non-linearity.

References

• What is the network structure inside a Tensorflow Embedding Layer? by Coderina, 2021

quotient-remainder-embedding-dealing-with-categorical-data-in-a-dlrm-a-paper-review