In this post, we shall see the simple yet powerful attention mechanism used in an encoder-decoder architecture that enables us to solve common time(sequences) dependent problems like

• Speech Synthesis
• Neural Machine Translation
• Multi Horizon Forecasting etc

In one of our previous posts, we briefly dealt with the mathematical intuition behind Attention in the context of bilogical inspiration. This post elaborates the attention mechanism and it’s simplicity that yields the desired result quite efficiently. Please refer,

• Higher Cognition through Inductive Bias, Out-of-Distribution and Biological Inspiration

Image Credit: Finding Your Focus Through ‘Deep Work’

You've been runnin' round, runnin' round, runnin' round throwin' that dirt all on my name
'Cause you knew that I, knew that I, knew that I'd call you up
You've been going round, going round, going round every party in L.A.
'Cause you knew that I, knew that I, knew that I'd be at one, oh

$ \ \ \ \ \ \cdots$

You just want attention, you don't want my heart
Maybe you just hate the thought of me with someone new
Yeah, you just want attention, I knew from the start
You're just making sure I'm never gettin' over you

you've been runnin' round, runnin' round, runnin' round throwing that dirt all on my name
'Cause you knew that I, knew that I, knew that I'd call you up
Baby, now that we're, now that we're, now that we're right here standing face-to-face
You already know, already know, already know that you won, oh

- Charlie Puth, Attention

It looks attention is truly a concept of recurrence, Charlie Puth is repeating words with various modulation like a Recurrent Neural Net failed to learn from the sequential Jacobians while predicting current outcomes and getting stuck.

Objective

Objective of this blog is to find answers to the following questions

• What is attention?
• What is memory?
• Mathematical intuition behind attention
• What is multi-head attention?
• Compute complexity of attention
• Experiments to prove simplicity and powerful nature of attention mechanism

Introduction

In human cognitive system attention is, pursue one line of thought over an n other and remain in focus. In deep learning, thought of interest is analogous to the network’s current state vector stored in the memory, which is choosing to look some part of that memory over an other.

Then the natural question is, what is memory? Memory is nothing but attention over time. i.e We have to store the state vector of interest through certain sophisticated data structure(e.g. key-value pairs) for faster retrieval in the future.

A memory augmented feed-forward neural network with an interesting concept called heads, heads are the parametric functions that writes and read selected memories based on the external input to produce the output. The efficiency of that network is determined by it’s ability to select portions of memory to write for a given external data to form an external output.

The process of learning when and where to pay attention is solved during backpropagation of the differentiable function.

An attention function can be described as mapping a query and set of key-value pairs to an output, 
where the query, keys, values and output are all vectors. The output is computed as a weighted 
sum of the values, where the weight assigned to each value is computed by a compatibility 
function of the query with the corresponding key.
- Vaswani et al, Attention is All You Need

Mathematical Intuition

Attention mechanism is employed to learn long-term relationship across different time steps. The simplicity of this scheme is sublime.

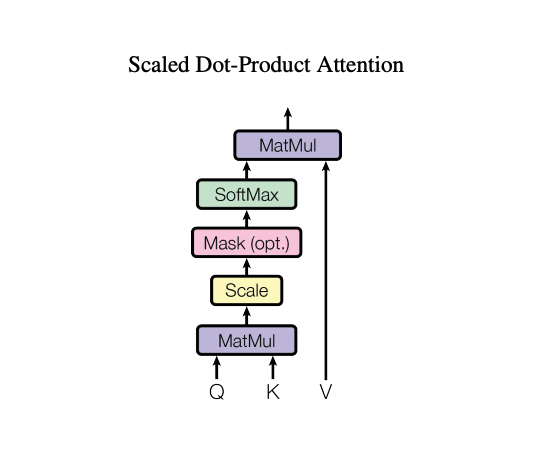
Image Credit: Attention Is All You Need

The Q, K and V

• Attention mechanisms scales values ${V} \in \mathbb{R}^{N \times d_v}$ relationship between keys(K) and queries(Q)
• $K \in \mathbb{R}^{N \times d_{attn}}$ is the Key
• $Q \in \mathbb{R}^{N \times d_{attn}}$ is the Query

$$Attention({Q, K, V}) = A({Q,K})V\tag{1}$$

Where,

• $A()$ is the normalization function - A common choice is scaled dot-product attention

$$A({Q,K}) = softmax \left(\frac{QK^T}{\sqrt{d_{attn}} } \right)\tag{2. Attention}$$

The simplicity I celebrated in the opening note of this post lies in the $Q\odot K^T$ part of the above equation and the denominator $\sqrt{d_{attn}}$ is a normalizing factor.

Also $Q$ is not a single query vector, It is again a matrix packed with multiple queries. $eqn.2$ The softmax transcendental function is nothing but a similarity calculator, like cosine similarity that identifies the right key $K$ for given $Q$ queries.

Multi-Head Attention

Multi Head Attention is proposed in employing different heads for different representation subspaces to increase the learning capacity. i.e Learning is happening in parallel for different contexts.

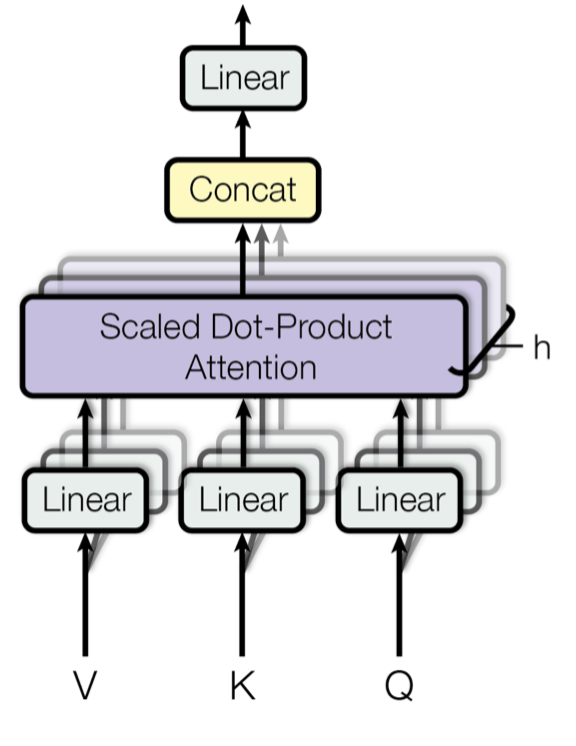
Image Credit: Attention Is All You Need

$$MultiHead{(Q,K,V)}) = [H_1, \cdots, H_{m_H}]W_H\tag{3}$$ $$i.e.$$ $$H_h = Attention(QW^{(h)}_Q, KW^{(h)}_K, VW^{(h)}_V) \tag{4. Multi-Head Attention}$$

Where,

• $W_K^{(h)} \in \mathbb{R}^{d_{model} \times d_{attn}}$ is head specific weights for keys
• $W_Q^{(h)} \in \mathbb{R}^{d_{model} \times d_{attn}}$ is head specific weights for queries
• $W_V^{(h)} \in \mathbb{R}^{d_{model} \times d_{V}}$ is head specific weights for values

We are trying to map sequences to sequences to predict the $i$th element of the right side sequence. In this scenario, we have to prevent leftward information flow in the decoder to preserve auto-regressive property. Hence the right elements are masked out before applying the softmax.

Image Credit: Long Short-Term Memory-Networks for Machine Reading

• Blue indicates the intensity of the activation
• Red indicates the current word to predict
• Green strikeout represents the masked words to prevent leftward information flow

Compute Complexity

The $Q\odot K^T$ operation looks computationally quite daunting because we are multiplying every element of the matrix that lead to $O(n^2.d)$ complexity. Where $n$ is the length of the sequence and $d$ is the representation dimension. Meanwhile, an attention model does not have any recurrent or convolution layers, makes it a mere positional connection with constant number of sequentially executed operations.

It is a rare event where the length of the sequence$(n)$ exceeds the representation dimension$(d)$, ensures the total computational complexity of attention mechanism far lesser than a recurrent model with a per layer complexity leads to $O(n.d^2)$. Complexity further reduces when the self attention mechanism restricts the size of the query with a focused set of input tokens.

Experiments

We shall implement the attention mechanism in an isolated environment using sythetic data. i.e. We are simplifying the problem by avoiding the complex neural network layers and real world data to focus on the efficacy of Attention mechanism.

In this implementation, we are skipping the normalizing factor $\sqrt{d_{attn}}$ in the denominator of $eqn.2$

import numpy as np
def attention_score(query, keys):
    return np.dot(query, np.transpose(keys))
def softmax(x):
    x = np.array(np.squeeze(x), dtype=np.float128)
    exp = np.exp(x)
    return exp / exp.sum(axis=0) 

Synthetic Data: Sequences

Let us create few known sequences and stack them to form the key value pair dictionary. Here the keys are generated as a random sequences with a specified length and the queries are picked randomly from the sequence vector and attention scores are calculated. The keys sequence vector symbolically represents the tokens of a word corpus or events of a time series. Their range is constant and not replaced while sampling.

SEQ_LEN = 6
REPRESENTATION_DIM = 5

def create_synthetic_sequences(seq_len=SEQ_LEN, representation_dim=REPRESENTATION_DIM):
    a = np.arange(seq_len)
    keys = [a.copy()]
    for idx in np.arange(representation_dim):
        np.random.shuffle(a)
        keys.append(a.copy())
        
    return np.array(keys)

keys = create_synthetic_sequences()
keys

array([[0, 1, 2, 3, 4, 5],
       [5, 3, 0, 4, 2, 1],
       [4, 2, 1, 0, 5, 3],
       [3, 0, 4, 2, 5, 1],
       [1, 3, 5, 4, 0, 2],
       [5, 3, 4, 0, 1, 2]])

Test 1, Random Pick from Keys

• Pick a random key from the keys vector
• Expand the dimension and make the query vector
• Calculate the attention score
• Softmax the attention score to get attention weights
• Identify the argmax of the attention score and compare with the index of the key randomly picked

query_idx = np.random.choice(np.arange(REPRESENTATION_DIM), 1)[0]
query = np.expand_dims(keys[query_idx], axis=0)

def test_attention(query, keys, query_idx):
    
    attention_scores = attention_score(query, keys)
    attention_weights = softmax(attention_scores)
    print(f'Query Index: {query_idx}, Attention Scores: {attention_scores}, Key Index Identified: {np.argmax(attention_scores)}')
    print(f'Is attention score matching: {np.allclose(np.argmax(attention_scores), query_idx)}, \nIs attention weight matching: {np.allclose(np.argmax(attention_weights), query_idx)}')
    
test_attention(query, keys, query_idx)

Query Index: 2, Attention Scores: [[39 39 55 44 21 41]], Key Index Identified: 2
Is attention score matching: True, 
Is attention weight matching: True

Test 2, Modify the Query

This test is similar to test 1 but the query is slightly modified to prove the query-key pattern is not exact.

query_idx = np.random.choice(np.arange(REPRESENTATION_DIM), 1)[0]

# Modify the query slightly
sign = np.random.choice([-1, 1], 1)[0]
query = keys[query_idx] + sign * np.sin(30)

test_attention(query, keys, query_idx)

Query Index: 4, Attention Scores: [49.82047436 46.82047436 35.82047436 47.82047436 69.82047436 52.82047436], Key Index Identified: 4
Is attention score matching: True, 
Is attention weight matching: True

Test 3, Query Modified and Swapped

In this test, modify the query and swap 2 items in the query

query_idx = np.random.choice(np.arange(REPRESENTATION_DIM), 1)[0]

# Modify the query slightly
sign = np.random.choice([-1, 1], 1)[0]
query = keys[query_idx] + sign * np.sin(30)
print(f'Actual Query: {query}')
# Swap positions
pos1, pos2 = np.random.choice(np.arange(SEQ_LEN), 2, replace=False)
query[pos1], query[pos2] = query[pos2], query[pos1]
print(f'Swapped Query: {query}')

test_attention(query, keys, query_idx)

Actual Query: [ 3.01196838  1.01196838  0.01196838 -0.98803162  4.01196838  2.01196838]
Swapped Query: [ 3.01196838  4.01196838  0.01196838 -0.98803162  1.01196838  2.01196838]
Query Index: 2, Attention Scores: [15.17952564 27.17952564 31.17952564 14.17952564 15.17952564 32.17952564], Key Index Identified: 5
Is attention score matching: False, 
Is attention weight matching: False

Test 4: Large Sequences and Representation Dimension

In this test, we increase the sequence length to 100 and representation dim to 1000 to demonstrate the robustness of the idea. In language models a sentence may not exceed beyond 30 or 40 words but other use cases like forecasting or speech synthesis might have larger sequence lenghts. This will cause higher computation cost and care must be taken while designing such systems.

SEQ_LEN = 100
REPRESENTATION_DIM = 1000
keys = create_synthetic_sequences(seq_len=SEQ_LEN, representation_dim=REPRESENTATION_DIM)
keys.shape

(1001, 100)

query_idx = np.random.choice(np.arange(REPRESENTATION_DIM), 1)[0]

# Modify the query slightly
sign = np.random.choice([-1, 1], 1)[0]
query = keys[query_idx] + sign * np.sin(30)
# Swap positions
pos1, pos2 = np.random.choice(np.arange(SEQ_LEN), 2, replace=False)
query[pos1], query[pos2] = query[pos2], query[pos1]


test_attention(query, keys, query_idx)

Query Index: 463, Attention Scores: [249888.75653926 246695.75653926 254062.75653926 ... 258536.75653926
 240208.75653926 251288.75653926], Key Index Identified: 463
Is attention score matching: True, 
Is attention weight matching: False


<ipython-input-1-43bfaa001364>:6: RuntimeWarning: overflow encountered in exp
  exp = np.exp(x)
<ipython-input-1-43bfaa001364>:7: RuntimeWarning: invalid value encountered in true_divide
  return exp / exp.sum(axis=0)

Weight matching resulted false only because of the nature of the synthetic data we have created. In real world, data will fit in gamut to calculate softmax without a failure.

Inference

I wanted this post to be as simple as possible, so that the core intuition behind attention mechanism is rendered for anyone with a curiosity to learn. Attention is quite famous and widely adopted for most of the AI problems because of it’s simplicity. It’s a pleasure to write this article and making is simple and portray it’s power with significantly less compute complexity. This is one of a kind concept and state of the art algorithm, I hope our AI community invents such algorithms more frequently in the future.

Reference

• Attention Is All You Need Vaswani et al, NeurIPS 2017
• Feed-Forward Networks with Attention Can Solve Some Long-Term Memory Problems Raffel et al, ICLR 2016
• Teaching Machines to Read and Comprehend Hermann et al, 2015
• Neural Machine Translation By Jointly Learning to Align and Translate Bahdanau et al, 2016
• Long Short-Term Memory-Networks for Machine Reading Cheng et al, 2016
• Deep Learning 7. Attention and Memory in Deep Learning by Alex Graves, Research Scientist @ Deep Mind, 2018
• Attention is all you need; Attentional Neural Network Models by Lukasz Kaiser @ PI Institute Master Classes, 2017
• Sequence to Sequence Learning with Neural Networks by Sutskever, NeurIPS 2014
• Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation by Cho et al, EMNLP 2014
• What Exactly Is Happening Inside the Transformer
• Attention? Attention! by Lilian Weng, 2018
• Attention in Neural Networks - 1. Introduction to attention mechanism by Buomsoo Kim, 2020