In this post, we study the fundamentals of graphs and graph neural networks and their key applications. GNN is an important topic in the AI world and is yet to have wide acceptance in the industries by realizing tangible work products. I believe this is the first post of a new series on Graphs and Graph Neural Networks that I am quite excited to share with you all.

• Image Credit: Knowing Your Neighbours: Machine Learning on Graphs

Objectives

The key objective of this post is to make a quick survey of the need and challenges in achieving GNNs, it’s significance in current times. We shall also study the mathematical intuition behind constructing a simple GNN and the applications of GNNs during the course.

Introduction

The term Graph Neural Networks(GNN) was coined first by Scarselli, Gori et al in their 2009 paper titled The Graph Neural Network Model published in the IEEE Transactions on Neural Networks - makes it GNNs are not something recent that bestowed upon us in the postmodern era of Attentions and Auto Encoders of the AI world. We collect gazillions and more volume of data but do we represent and store them in a way that is intuitive for the current needs - my conclusion is, mostly No.

I take this opportunity to trumpet the eminence of JSON representation, especially in web technologies. The fundamental reason for JSON’s success in rendering objects on the 2-dimensional space is its dexterity to represent space with agility, we call it JSON tree, no? A seasoned designer with a piece of foundational knowledge on JSON can translate the data into UI objects and experiences like time-motion effortlessly.

This is possible because of the proximity of the representation to experience. However, the tabular representation distributes information across multiple entities in that process lose its intuitiveness - Hence we transform the data from table to tree when we render. A relational database is not truly relational but just an idea, a primitive form far away from reality. On contrary, a graph with its edges and vertices describes the relationship as a relationship with superior proximity to reality.

Graph Data

A graph is a data structure consisting of vertices and edges where vertices are a set of nodes and the edges are the relationship between them. The terms nodes and vertices are interchangeably used. If two nodes have directional dependencies their edges are directed otherwise, they are undirected.

Adjacency Matrix:
Graphs are represented using a matrix called adjacency matrix, again a tabular form. i.e If a graph has $n$ vertex then the shape of the adjacency matrix is $(n \times n)$.

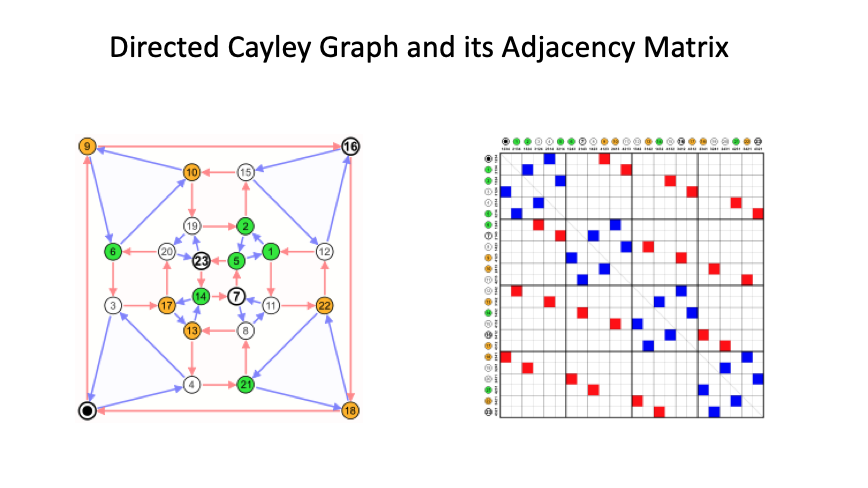
• Image Credit: Adjacency Matrix @ Wikipedia

Challenge is graphs are complex and it manifests when it comes to machine learning because ML algorithms assume observations are independent of each other. This assumption is not applicable for graph data because the vertices are related to each other.

The reason is that conventional Machine Learning and Deep 
Learning tools are specialized in simple data types. Like 
images with the same structure and size, which we can 
think of as fixed-size grid graphs. Text and speech are 
sequences, so we can think of them as line graphs.

- Amal Menzli, 2021

Adjacency Matrix representation of a graph is simple to comprehend and easy to process, meanwhile it is once again the conventional way of representation inspired from the spreadsheets. We find graphs everywhere Social Networks, Product Categorization, Organization Charts, Citations, etc are few to name. Our conventional perception of the image is a rectangular grid with image channels in the form of flattened arrays. We can represent images as graphs by considering each pixel as a node, that node is connected to its neighbors using an edge. This approach enables us to gather the relationship among the pixels in a connate way. However, this approach results in the redundancy of data at every node level.

Utility of Graph Networks

Mostly we seek the help of ML algorithms for regression and classification problems for diverse domains, using GNNs we will be doing similar tasks at 3 levels,

1. Graph Level Tasks
2. Node Level Tasks
3. Edge Level Tasks

Graph level tasks are to predict the character of the entire graph. For e.g. we have a social network graph for LinkedIn which is independent of Twitter or Facebook. Graph level tasks assist us in identifying whether the network is a professional social network or a photo-sharing social network.

A node-level task helps us to identify the role of a node within the boundary of a graph. For e.g A family WhatsApp group where everyone is connected to each other(a homogenous network). In this graph, we can identify which Maami(a middle-aged or an elderly woman) is most influential and which one is least among the family member.
Image segmentation task can be seen as a node-level task - we identify the role of each pixel.

• Image Credit: The Network Effects Bible - Homogeneous vs. Heterogeneous Networks

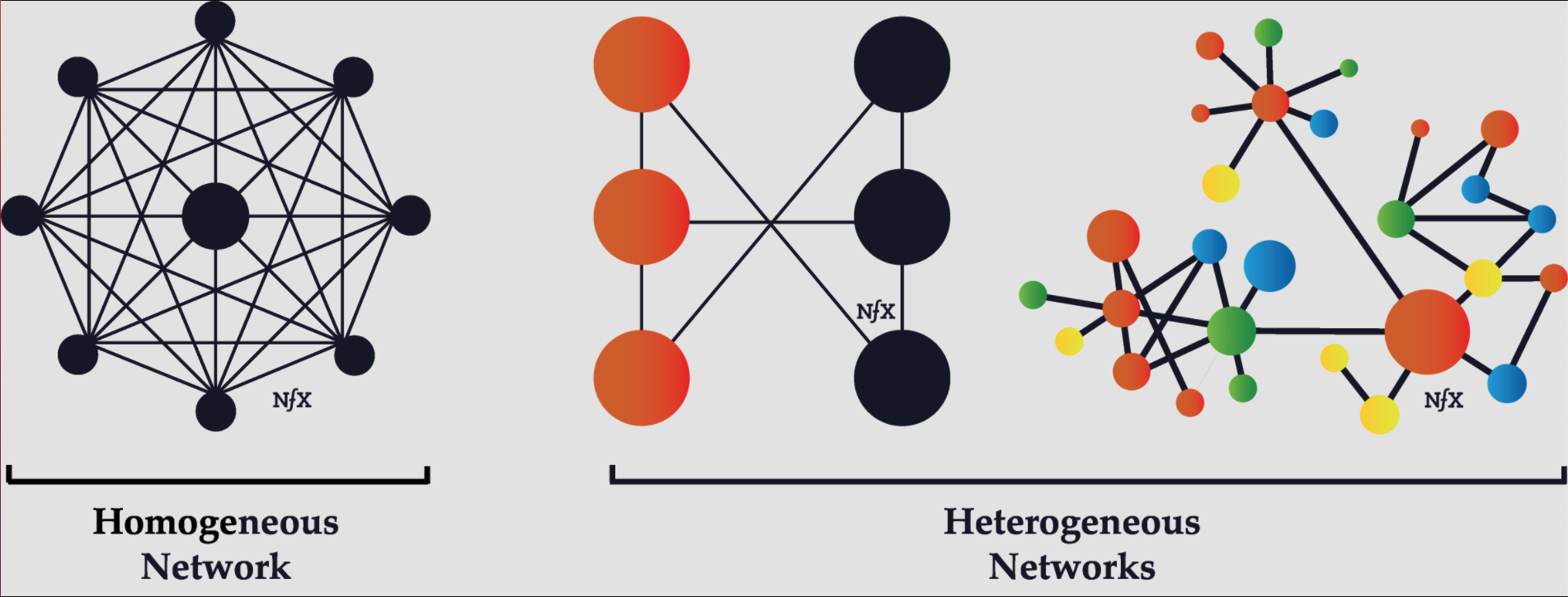
An edge-level task is to identify the relationship between two nodes. For e.g. in an organization, the proximity of an employee to the key decision-maker would be making him/her an influential person. Edge level tasks can quantify and classify the relationship between nodes.

One example of edge-level inference is in image scene understanding. Beyond identifying objects
in an image, deep learning models can be used to predict the relationship between them. We can 
phrase this as an edge-level classification: given nodes that represent the objects in the 
image, we wish to predict which of these nodes share an edge or what the value of that edge is. 
If we wish to discover connections between entities, we could consider the graph fully connected
and based on their predicted value prune edges to arrive at a sparse graph.

- GNN Intro from Distil.pub

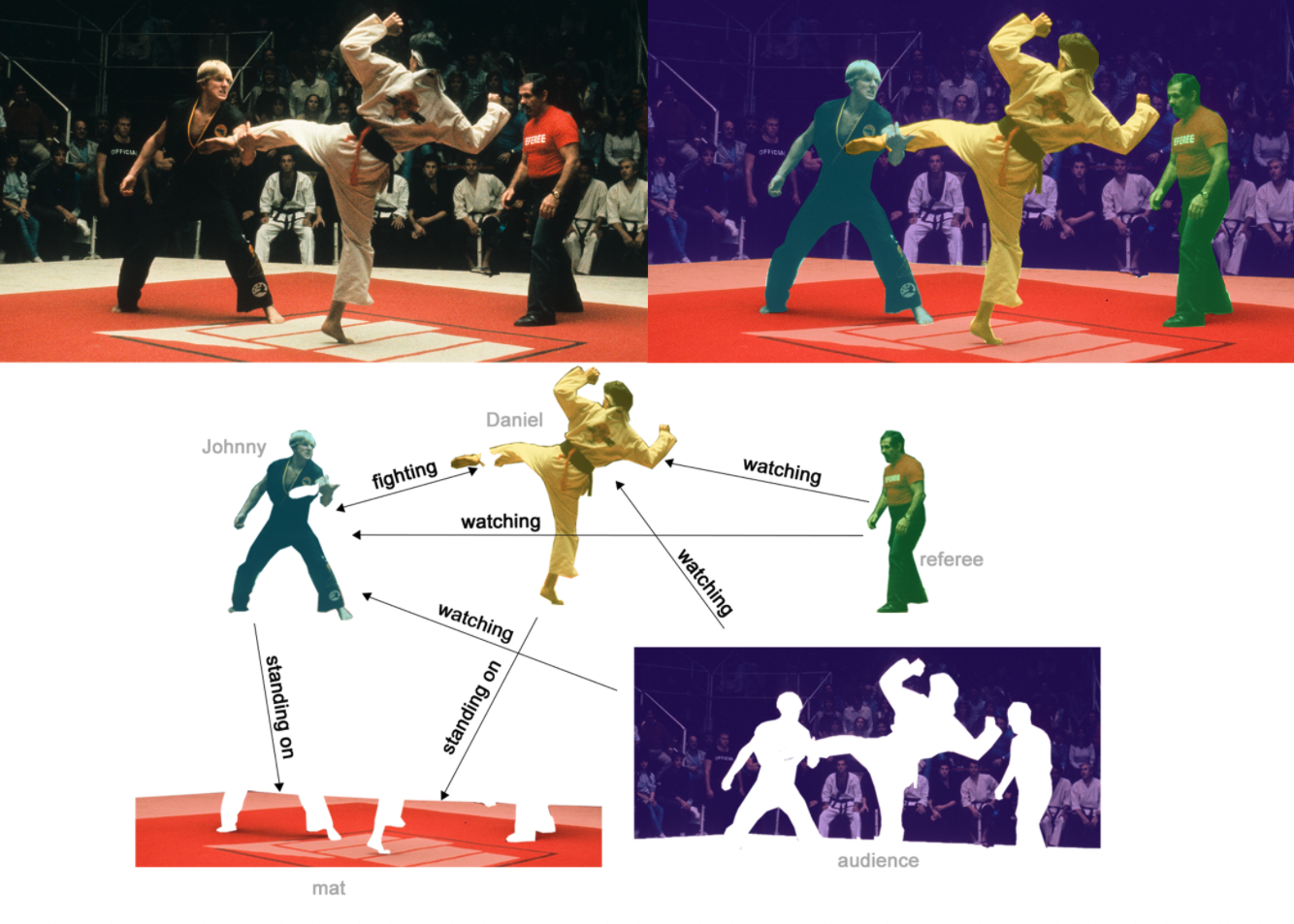In (b), above, the original image (a) has been segmented into five entities: each of the fighters, the referee, the audience and the mat. (C) shows the relationships between these entities.

• Image Credit: A Gentle Introduction to Graph Neural Networks

Graph Representation

Graph data structures stores 4 different types of information that are critical to building our deep learning systems,

1. Nodes
2. Edges
3. Global Context and
4. Connectivity

The representation of the first 3 of 4 attributes is significantly easy but not the connectivity information. Let us assume a graph of million nodes(e.g. social networks), constructing a $(million \times million)$ adjacency map is practically impossible due to space constraints. Further, there is a chance of redundant adjacency matrices to describe every possible permutation of the connections among the nodes.

$$O(n_{nodes}^2) \tag{1. Space Complexity of Adjacency Matrix}$$

Adjacency maps are ruled out and we seek the help of an adjacency list to describe the connectivity, using significantly smaller space. Adjacency lists describe the connectivity using a list of tuples that result in smaller compute and storage complexity. $$O(n_{edges}) \tag{2. Space Complexity of Adjacency List}$$

Graph Neural Networks

The objective of a Graph Neural Network is to apply neural network processing directly to the graphs and provide an edge, node, and graph-level prediction tasks. To understand the challenges, let us take the example of convolution neural networks(CNNs). The key concept that paved the way for the success of CNNs is the spatial locality, i.e. Convolution and Pooling are applied to identify spatially localized features through a set of receptive fields(kernels).

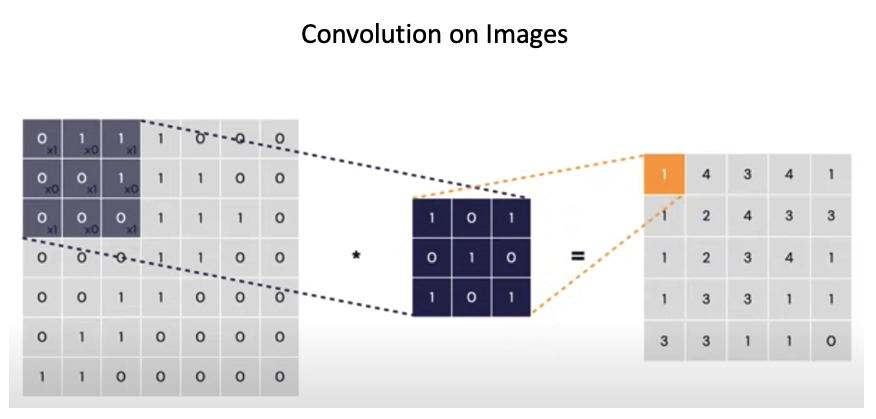
Let us take the localization inspiration of CNNs for graph networks - a graph convolution network(GCN) that is quite similar to CNN for the simple reason that it considers the immediate neighborhood of a particular node to update the node’s features.

A GNN is an optimizable transformation on all attributes of the graph 
(nodes, edges, global-context) that preserves graph symmetries 
(permutation invariances).

- GNN Intro from Distil.pub

$$\vec{h_i^l} = f(\vec{h_a}, \vec{h_b}, \vec{h_c}, \cdots, \vec{h_i})$$

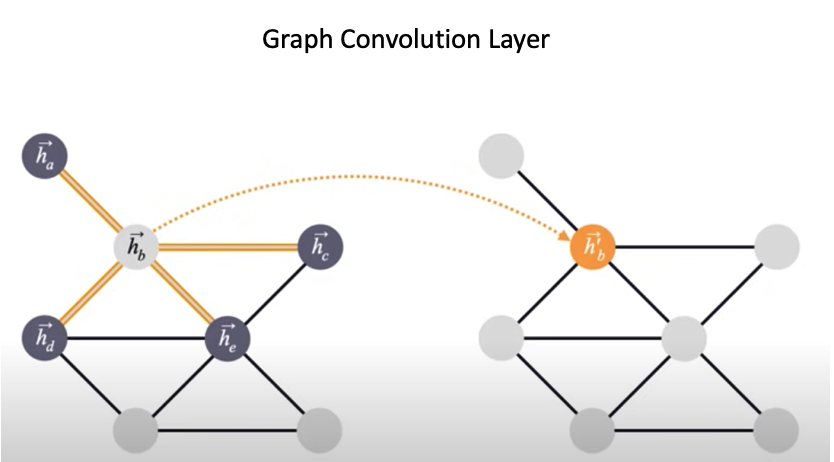
Trivia:

• This spatial localization is not possible in graph representation and the depth of the graph is arbitrary due to the complex topological structure. Since there is no spatial localization, there is no direct Euclidean geometry to calculate the loss during training.
• There is a need for defining different importances to different neighbors.
• However, we rely on our fundamental principle of similarity measures for the nodes - so that we can juxtapose similar nodes in the embedding space and dissimilar nodes far away from each other.

Simple GNN using Adjacency Matrix

In this section, we shall build a simple GNN using adjacency matrix with following assumptions. The graphs are unweighted and undirected(symmetric), so that our representation matrix has ${0, 1}$ i.e $A_{ij} = A_{ji} 1 \rightarrow i \leftrightarrow j, 0 \ otherwise$. then, $$H’ = \sigma(AHW) \tag{Aggregation of Neighbor Nodes}$$

• $W$ is a learnable node-wise shared linear transformation
• $\sigma$ is sigmoid for non-linearity The above process recombines the information in the neighbor nodes into one vector. It allows us to enable layered processing, instead of $\sigma$ we can use $ReLU$ to represent complex features.

An identity matrix is added to the central node so that the context of the central node is preserve. $$\tilde{A} = A + I \tag{Ensures the node is always connected to itself}$$ then the node-wise update rule can be written as $$\vec{ h_i^{\prime}} = \sigma \left ( \sum_{j\in N_i}W\vec{ h_i}\right) \tag{Pooling of Neighbors}$$

Multiplication of Adjacency matrix result in scaling up the output features, hence we normalize the features so that they are do not explode by multiplying the inverse of the degree of the matrix as follows, $$H^{\prime} = \sigma(\tilde{D}^{-1}\tilde{A}HW)$$

Where,

$$\tilde{D}{ii} = \sum_j \tilde{A}{ij} \tag{Degree of the matrix A}$$

$$\vec{ h_i^{\prime}} = \sigma\left(\sum_{j\in N_i}\frac{1}{|N_i|} W\vec{ h_i}\right) \tag{Mean Pooling of Neighbors}$$

Conclusion

Learning GNNs is a long pending task that I kept on postponing until I got an invite to attend the GNN workshop from Stanford University last week. The first half of the workshop was interesting and the Stanford team demonstrated the PyG package in detail. I could follow what is going on at a very high level but not to an extent of understanding the math behind the scenes. Hence, I decided to take a plunge and spent some time on Graphs and Graph Neural Networks. This post renders the graph representation of data and the challenges in detail. It also emphasizes how a graph representation is closer to nature compared to a tabular or sequential way of representing data for deep learning problems. I am glad I could cover the math for GNN at a very high level in this short post. From here, I plan to focus on studying

1. Graph Convolution Network(GCN) in detail,
2. Message Passing Neural Networks(MPNN)
3. GNNs without Adjacency Matrices etc

Hope you all enjoyed this write-up. If you have any comments, compliments or curses - Please drop a message.

References

• Graph Neural Network and Some of GNN Applications – Everything You Need to Know by Amal Menzli, 2021
• A Gentle Introduction to Graph Neural Networks
• Semi-Supervised Classification With Graph Convolutional Networks by Kipf and Welling, ICLR 2017
• Graph Convolutional Netowrks by Thomas Kipf, 2016
• Intro to graph neural networks (ML Tech Talks) by DeepMind’s Petar Veličković, 2021
• Graph neural networks: A review of methods and applications by Zhou et al, 2020
• The graph neural network model by Scarselli et all, 2009
• A Gentle Introduction to Graph Neural Networks (Basics, DeepWalk, and GraphSage) by Hsiang et al, 2019