Introduction to Contrastive Loss - Similarity Metric as an Objective Function
Posted January 30, 2022 by Gowri Shankar ‐ 6 min read
My first machine learning work was based on calculating the similarity between two arrays of dissimilar lengths. The array items represent features of handwritten characters extracted from a 2D vector captured using an electronic pen at a certain frequency, Circa 2001. The fundamental idea behind the similarity calculator is the measure of Euclidean distance between feature vectors of the corpus and the observed character strokes. Then came the most famous Siamese neural network architecture(~2005) that has two or more identical networks with the same parameters and weights that measure the similarity by comparing feature vectors of the input images. Semantic similarity calculations using distance measure is the way to go when we do not have labeled(or partially labeled) data with a very large number of objects to classify/detect. The similarity metrics can be used to compare and identify unseen categories when the data evolves. i.e If it walks like a duck and quacks like a duck, we prefer to infer it is a duck even if our training data had never seen a duck.
Face recognition is the classic application of contrastive learning models, there we have evolved from PCA-based architectures that are sensitive to geometric attributes like scale, rotation, etc, and tackled variabilities like spectacles, accessories, and emotions. This post explores the fundamentals of contrastive learning and an energy-based approach towards arriving at decision boundaries. This post falls under Fundamentals of AI/ML and `Energy-Based Models,
Objective
The objective of this post is to introduce contrastive loss functions and the need for them in an intuitive way.
Introduction
State-of-the-art vision models for classification and object detection are built on the Cross-Entropy loss function as the objective function in the arena of supervised learning. These models are not only efficient but widely accepted among the deep learning communities. However, there are quite a few issues and shortcomings with the cross-entropy loss function that made the community think beyond the boundaries. The primary goal is to increase the robustness, strive toward achieving generalization goals, handle noisy data, etc. Furthermore, the problems with supervised learning are humongous. The issue of annotation and labeling where human dependence is a time bomb waiting to blast, the most concerning issue is the bias among the human annotators. Hence, there is a wide acceptance that self-supervised learning is the way forward for meaningful, AI if not AGI.
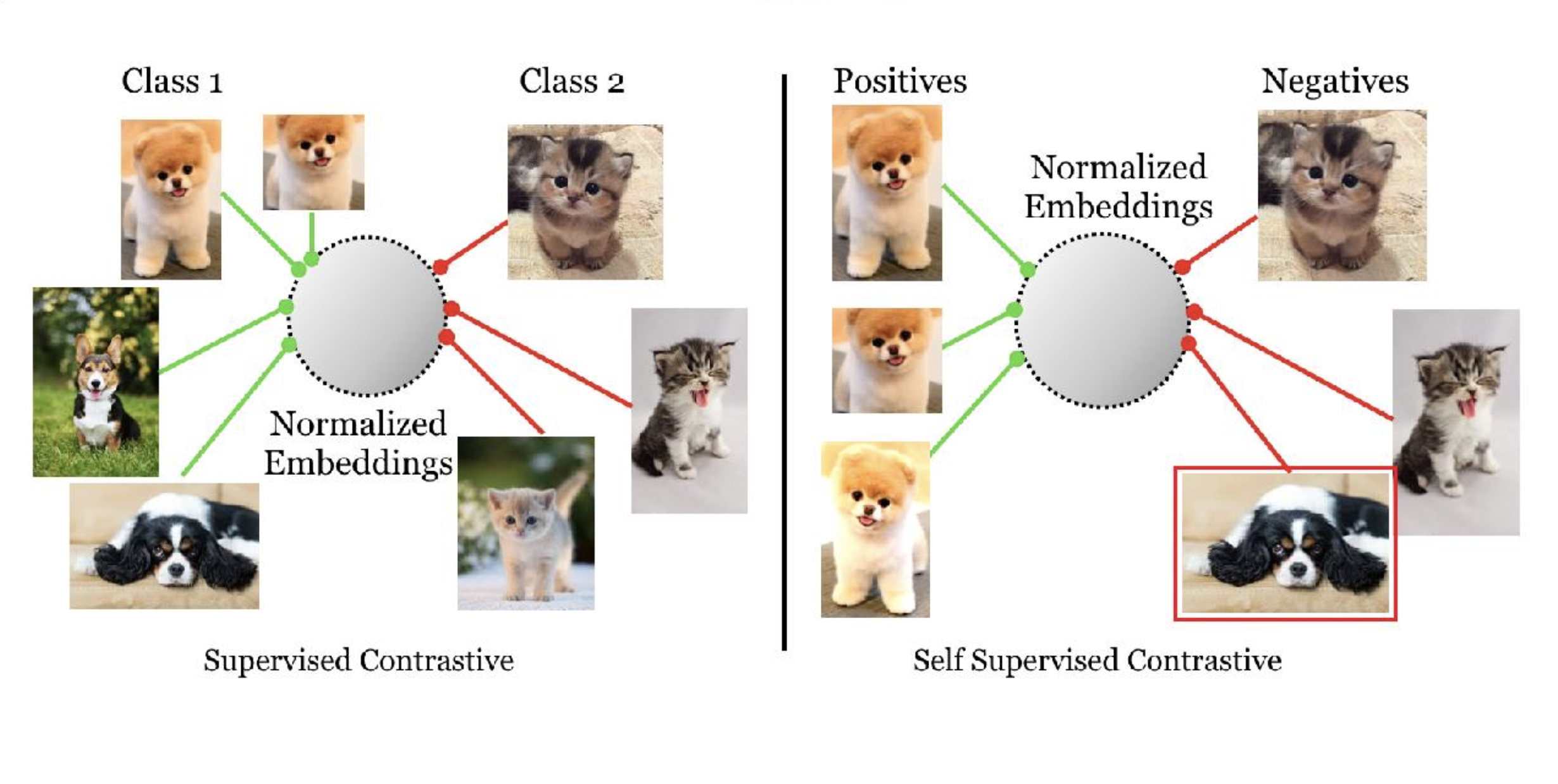
When it comes to self-supervised representation learning, contrastive learning and loss functions make a significant impact on model explanation and interpretability. Let us say we have an anchor image in the dataset and a positive sample is generated using data augmentation techniques then the positive samples are pulled towards the anchor and the negatives are pushed far away from the positives. The logic behind this process is the maximization of mutual information between different snapshots of the training data. The
Normalized embeddings from the same class are pulled closer
together than embeddings from different classes.
- Khosla et al, Google Research
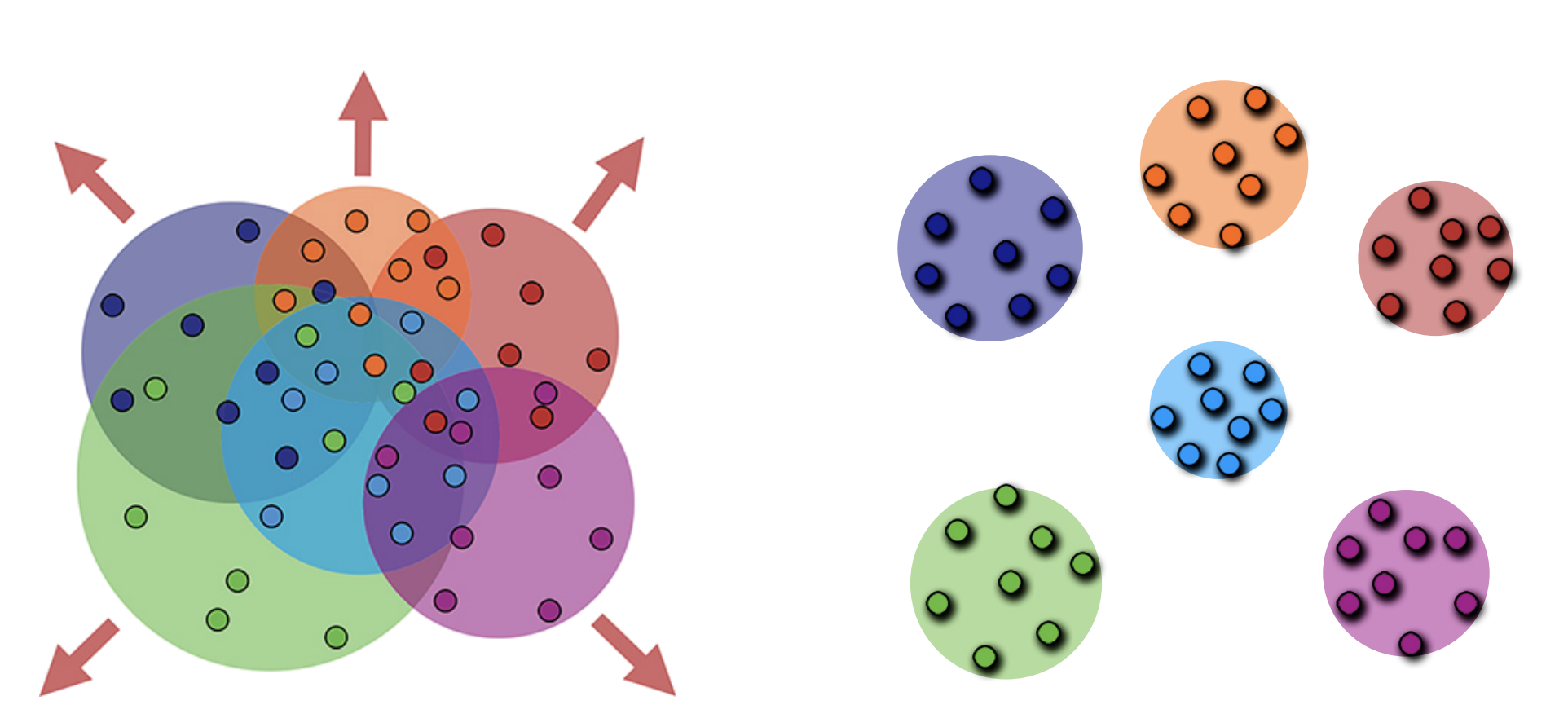
- Image Credit: Metric Learning with Adaptive Density Discrimination
Contrastive loss functions have a rich history in their evolution, they are primarily designed based on how they handle the images by comparing with one another. E.g. Siamese network had 1 positive and 1 negative per reference anchor. The following are the few other contrastive loss functions,
- Triplet Loss: One positive and one negative sample per anchor image
- N-Pair Loss: One positive and many negative samples for an anchor image
- Recent Developments(e.g. SupCon): Many positives and many negative samples for an anchor image
Cross Entropy
We strongly believe that contrastive loss is much better than cross-entropy loss because of its ability to differentiate two objects. This capability is critical in the self-supervised learning setup where the challenges with annotation-related issues can be easily circumvented. It is my discomfort when I see an image is mapped to a particular object, I believe an image is much more than a single(or known) object. At some point, our AI models should evolve to consider the context and conditions for better inference. E.g. there is a significant amount of difference between an image in which a human is chased by a dog and the one with a leopard. Imagine we did not have a class label for the leopard, most likely the model will infer it as a dog chasing a man. To be precise, how different a dog and a leopard are is the question that contrastive loss function as an objective function is expected to solve.
$$ E = - \sum_{i=1}^C q_c log p_c \tag{1. Cross-Entropy Loss}$$
Where,
- $q$ is a one hot vector of the classes
- $p_c$ denotes the probability of the vector belongs to class $c$
- $C$ is the total number of classes $$p_c = \frac{e^{u_c}} {\sum_{i=1}^C e^{u_i}} \tag{2. Softmax function}$$
- $u$ represents the vector of class $c$ When there are only 2 classes in the classification task we use binary cross entropy loss as follows $$E = -ylog(p) - (1-y)log(1-p) \tag{3. Binary Cross-Entropy Loss}$$
The goal of this setup is to minimize the cross-entropy loss and eventually to make the output closer to the one-hot vector $(u)$.
Contrastive Loss
The goal of contrastive loss is to discriminate the features of the input vectors. Here an image pair is fed into the model, if they are similar the model infers it as $1$ otherwise zero. We can intuitively compare it with the goals of cosine similarity as an objective function. Contrastive learning methods are also called distance metric learning methods where the distance between samples is calculated.
$$ E = \frac{1}{2} yd^2 + (1-y)max(\alpha - d, 0) \tag{4. Contrastive Loss}$$
Where,
- $d$ is the Euclidean distance between the image features
- $\alpha$ is the margin - Let us say if two images are similar, their distance should be greater than the margin.
Triplet Loss
In triplet loss, we have 3 images
- An anchor($I_a$),
- A Positive($I_p$) and
- A negative($I_n$)
The goal is to maximize the distance between the difference of features between anchor, positive pair and the anchor, negative pair.
$$ E = max(||f_a - f_p||^2 - ||f_a - f_n||^2 + m, 0) \tag{5. Triplet loss}$$
In the above equation, is a margin term used to “stretch”
the distance differences between similar and dissimilar
pair in the triplet, is the feature embeddings for the
anchor, positive and negative images.
Jiedong Hao, 2017
Epilogue
In this post, we studied contrastive loss and the need for it. We also studied the difference between contrastive and cross-entropy losses. Triplet loss is just another flavor of contrastive loss that brings more robustness to the model. This topic is one of the precursors for diving deep into self-supervised models especially the energy-based models. Hope you all enjoyed this short read.
References
- Supervised Contrastive Learning by Khosla et al, 2021
- Learning a Similarity Metric Discriminatively, with Application to Face Verification by Chopra, LeCun et al 2005
- A friendly introduction to Siamese Networks by Sean Benhur, 2020
- Contrastive Loss Explained by Brian Williams, 2020
- Contrastive Representation Learning by Lilian Weng, 2021
- Improved Deep Metric Learning with Multi-class N-pair Loss Objective by Kihyuk Sohn, 2016
- Distance Metric Learning for Large Margin Nearest Neighbor Classification by Weinberger, 2009
- Extending Contrastive Learning to the Supervised Setting by Maschinot, 2021
- Learning Word Embedding by Lilian Weng, 2017
- Metric Learning with Adaptive Density Discrimination by Rippel et al, 2016
- Significance of Softmax Based Features Over Metric Learning Based Features by Horiguchi et al, 2017
- Some Loss Functions and Their Intuitive Explanations by Jiedong Hao, 2017
introduction-to-contrastive-loss-similarity-metric-as-an-objective-function