In this post, we shall see the mathematical intuition behind transforming discrete data to continuous ones using normalizing flows. Normalizing flows are not new to us, please refer to one of the past implementations of normalizing flows and the fundamentals of Bijective functions used for creating normalizing flows here.

• Bijectors of Tensorflow Probability - A Guide to Understand the Motivation and Mathematical Intuition Behind Them
• Normalizing Flows - A Practical Guide Using Tensorflow Probability

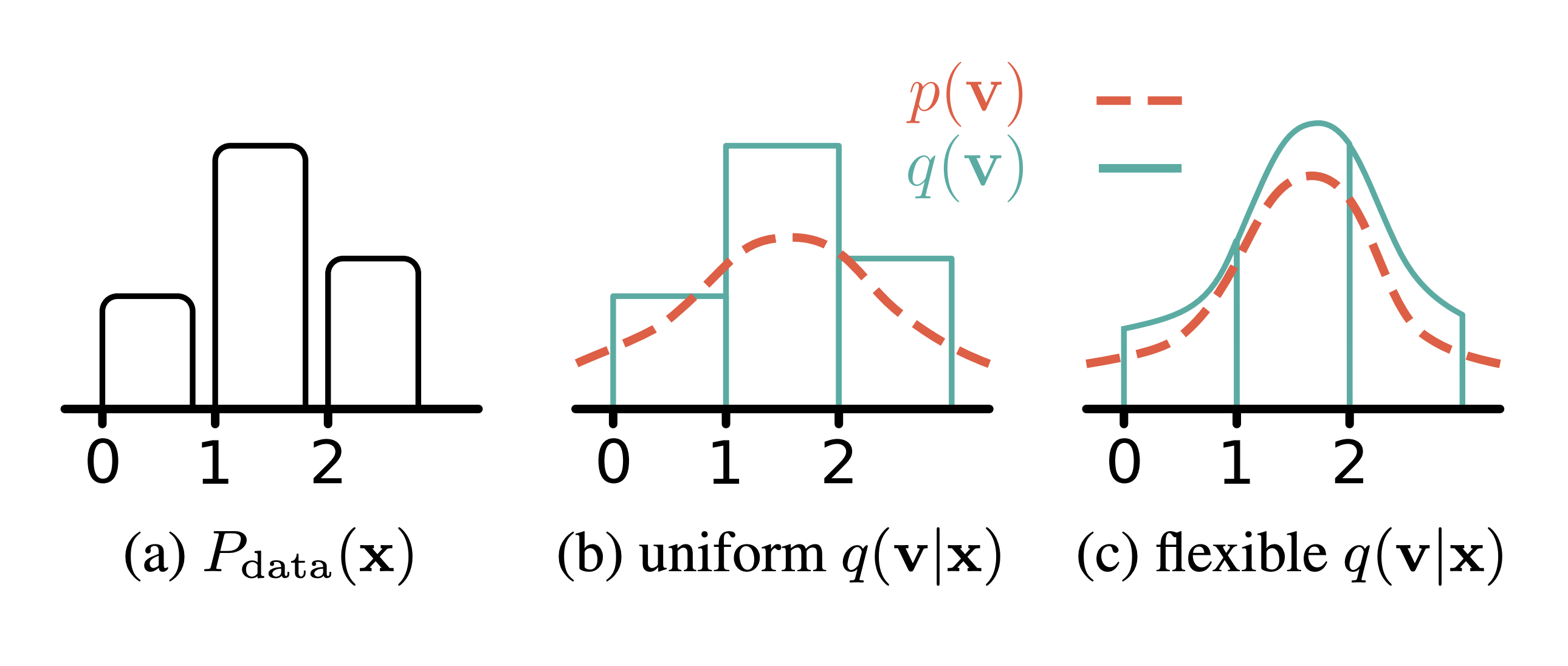
• Image Credit: Learning Discrete Distributions by Dequantization

Normalizing flows are phenomenal in vision and text(also speech) synthesis result in creating a newer distribution of realistic nature. The recent breakthrough applications are, AI completing Beethoven’s 10th symphony and realistic rendition images from text input of Samuel Taylor Coleridge’s poem Kubla Khan.

• Beethoven’s unfinished Tenth Symphony completed by artificial intelligence
• Coleridge’s “Kubla Khan”, rendered by machine learning models (CLIP/VQGAN).

This post is a review of Lippe and Gavves of University of Amsterdam paper title Categorical Normalizing Flows Via Continuous Transformations published as a conference paper at ICLR 2021.

Objective

The key objective of the post is to understand normalizing flow for any general case of categorical data. We also study the challenges involved in converting from discrete space to continuous space along with its mathematical background.

Introduction

Pixels of images are represented in 8 bit integers of order ${0-255}$ where the light intensity of 0 is relatively closer to 1 and far from 255 - i.e Image data is discrete and light intensity representaiton is ordinal. Hence, the transformation of images from discrete pixels to continuous distribution worked quite well to generate new images from GANs like architectures. i.e, $$p_{model}(x) \rightarrow p_{model}(x + u) \ where \ u \in [0, 1) \tag{0. Dequantization}$$

Where

• $u$ is a noise added to apply continuous normalizing flow on discrete data to get density models.
• $p_{model}$ is the distribution of the image
• $q(u|x)$ is a uniform distribution of the noise added to the image

The key issue in this process is the ordering of the pixel as integers that introduces bias to the representation make it practically impossible for this scheme to adopt other discrete representations of data where there is no intrinsic order(discrete and nominal).

When it comes to categorical data things are not as simple as discrete image representations, In the retail industry store identifier of consumer goods sales data or graph representation (nodes/edges) of molecular data for drug discovery are discrete. Those discrete representations result in tedious encoding because of their complex and multi-dimensional relationships. For example, two shops may be located nearby in the same area but they are specialized in selling different categories of products. Similarly, two atoms may be located nearby through a strong atomic bond but their neighboring atoms define the nature of the molecule to become significantly different. One other classic example is the words and their meanings.

Categorical Normalizing Flows - Definition

If you simplify the problem, the inherent nature of the discrete data with its discontinuities is to be transformed into a volume/density representation. i.e. Continuous encodings for discontinuities that is non-overlapping and close to deterministic volumes.

Variational inferencing is one of the widely considered schemes to approximate posteriors. The same technique is used to learn and infer the latent space $z$ where the discrete categorical data is represented.

Normalizing Flows - Continuous Data

A Normalizing Flow is a transformation of a simple probability distribution(e.g. a standard normal) into a more complex distribution by a sequence of invertible and differentiable mappings. The density of a sample can be evaluated by transforming it back to the original simple distribution says Kobyzev et al, in their paper Normalizing Flows An Intro and Review of Current Methods.

This mechanism makes it easy to construct new families of distributions by choosing initial densities and then chaining with parameterized, invertible, and differentiable transformations.

$$\Large z_0 \sim p_0(z_0) \tag{1. Base Distribution}$$

Where $p_0$ is the density of the base distribution.

Normalizing Flows should satisfy several conditions to be practical. They should:

• be invertible; for sampling we need function and for computing likelihood, we need another function,
• be sufficiently expressive to model the distribution of interest,
• be computationally efficient, both in terms of computing f and g (depending on the application) but also in terms of the calculation of the determinant of the Jacobian.

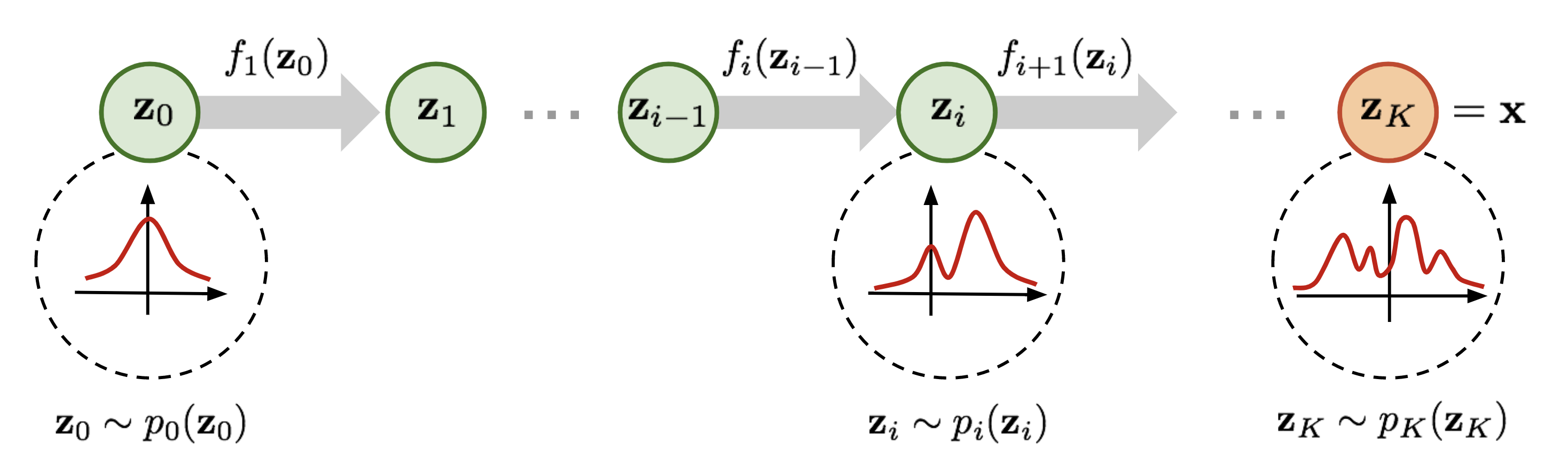Image Credit: Flow-based Deep Generative Models

Based on the figure which is an absolute representation of Kobyzev et al,

$$ z_{i-1} \sim p_{i-1}(z_{i-1}) \tag{2} $$

$$z_i = f_i(z_{i-1})$$ $$thus$$ $$z_{i-1} = f_i^{-1}(z_i)$$ $$from \ eqn.2$$ $$p_i(z_i) = p_{i-1}(f_i^{-1}(z_i))\left| det \frac{df_i^{-1}}{dz_i} \right| \tag{3}$$

In $eqn.3$ the basic rule for transformation of densities considers an invertible, smooth mapping $f: \mathcal{R}^d \rightarrow \mathcal{R}^d$ with inverse $f^{-1}$. This mapping is used to transform the random variable(simple distribution) to obtain a new density.

Applying the chain rule of inverse function theorem which is a property of Jacobians of invertible functions, we can construct arbitrarily complex densities by composing several simple maps of successive applications.

$$p_i(z_i) = p_{i-1}(z_{i-1})\left| det \left(\frac{df_i}{dz_{i-1}}\right)^{-1} \right|$$

We are dealing with very small numbers, hence we shall move to log spaces $$log p_i(z_i) = log p_{i-1}(z_{i-1}) + log \left| det \left(\frac{df_i}{dz_{i-1}}\right)^{-1} \right|$$

$$log p_i(z_i) = log p_{i-1}(z_{i-1}) - log \left| det \frac{df_i}{dz_{i-1}} \right| \tag{4}$$

the final term is the ‘determinant of the Jacobian’

Elementwise Flow: Intuition

We shall generalize the $eqn.4$, A normalizing flow consists of invertible mappings from a simple latent distribution $p_z(z)$ to a complex distribution $p_x(x)$. As we have seen before, $f_i$ be an invertible transformation from $z_{i-1} to z_i, z_0 = z$. Then the log-likelihood $log p_X(x)$ can be expressed in terms of the latent variable z based on the change of variables theorem.

$$z = f_1^{-1} \circ f_2^{-1} \circ \cdots f_k^{-1}(x) \tag{5}$$ $$from \ eqn.4$$ $$logp_X(x) = log p_Z(z) - \sum_{i=1}^k log \left| det \left( \frac{\partial f_i}{\partial z_{i-1}} \right) \right| \tag{6. Log Likelihood}$$

$eqn. 5, 6$ suggests that that optimization of flow-based models requires the tractability of computing $f^{-1}$ and $log \left| det \left( \frac{\partial f_i}{\partial z_{i-1}} \right) \right|$. After training, sampling process can be performed efficiently as follows

$$z \sim p_Z(z)$$ $$x = f_k \circ f_{k-1} \circ \cdots f_1(z) \tag{7}$$

NFs for Discrete Data

I would like to take the nationwide sales data of a consumer goods manufacturer as a case study for explaining normalizing flows for categorical data. Usually, a consumer goods company manufactures products of different categories, brands, etc sold to its customer base via distribution networks. In this dataset, the usual observation is that there are 3 continuous variables

• the volume of the sales measured in units,
• the value of the sales in local currency and
• the date of sales. Rest all pieces of information are categorical data, we are assuming it is the primary and secondary sales between the manufacturer to the retail outlet via the distributor. Let us say the sales data is $x = {x_1, x_2, x_3, \cdots, x_S}$ is multivariate in nature with more than one categorical column. Where each element $x_i in x$ is itself a categorical variable of K categories.

For example, the category of the product to be sold is a categorical column with more than 1 category of products in the lot. Further, products are classified into brands represent another categorical column. Similarly, the retail outlet that purchases the product from the manufacturer is classified into channels, sub-channels, etc. The goal is to learn the joint probability mass function $P_{model}(x)$ via a normalizing flow.

Before diving deeper, we have two functions encoders $q(z|x)$ that provides us the joint probability distribution of all the $S$ categorical variables of K different logistics for each we have in our data and decoders p(x_i|z_i) that decodes the latent space to discrete entities without any loss.

$$\Large q(z|x) = \prod_{i=1}^S g(z_i|\mu(x_i), \sigma(x_i)) \tag{8. Encoder}$$

$$p(x|z) = \prod_i p(x_i|z_i) \tag{9. Conditional Likelihood of the Decoder}$$ $$where$$ $$\Large p(x_i|z_i) = \frac {\tilde p(x_i)q(z_i|x_i)}{\sum_{\tilde x} \tilde p(\hat x)q(z_i|\hat x)} \tag{10. Decoder}$$

Where,

• $\tilde p(x_i)$ is prior over categories.

• Modeling complexity is solely in the prior to keep a lossless reconstruction of the latent space $z$ $$z_i \in \mathbb{R}^d \tag{9. Latent Space of the Stochastical Variable Mapped to x}$$

• The interaction of categorical variables $x$ are learned inside the normalizing flow

• The encoding of the categories is overlapped and the model cannot distinguish between all categories, hence the encoder is optimized to provide suitable representations of categorical variables.

• This is done by separating the different categories in the latent space.

• Decoder is incentivized to be deterministic while reconstructing $x$ from $z$

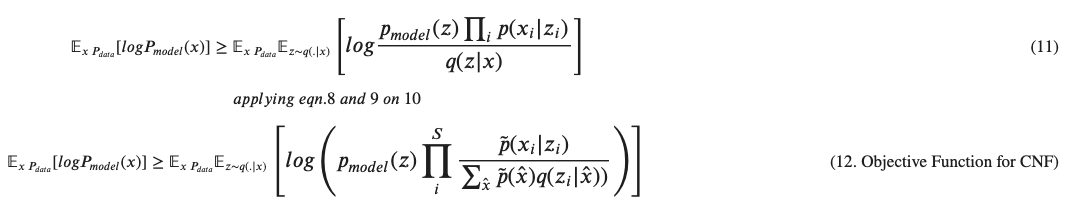
Elaborating Eqn. 8 - Mixture of Logistics

Equation 8. might have caused quite a bit of confusion, how on earth we can unearth a mean and standard deviation of nominal data. The mixture models represent each category by an independent logistic distribution in the $z$ space.

$$q(z|x) = \prod_{i=1}^S g(z_i|\mu(x_i), \sigma(x_i)) \tag{8. Encoder}$$ $$then$$ $$\Large g(v | \mu, \sigma) = \prod_{i=1}^d \frac {e^{- \epsilon_n}}{(1 + e^{-\epsilon_j})^2} \tag{13. Logistic Distribution}$$ $$where$$ $$\epsilon_j = \frac{v_j - \mu_j}{\sigma_j}$$

Where,

• $d$ is the dimensionality of the continuous latent space per category
• $\mu$ and $\sigma$ are learnable parameters, implemented via a table lookup

Conclusion

I doubt I understood this paper in full and I will do only when I hand-code myself every equation above. Meanwhile, I am glad I could comprehend the intent of the authors and their work at a certain level of clarity. Permutation invariant problems on categorical datasets are quite common, our representation and schemes of learning of nominal data in conventional machine learning models are quite primitive. Precisely, we do not know how to take advantage of the tressure of information hidden behind categorical values of higher dimensions. Often one categorical variable has a graph-like relationship with another one - this paper from UVA shred light on those problems and paves a promising path for learning complex relationships. Hope this write-up helped you all - for me, it is an adventure in an unknown territory, Good Bye until one more fearless adventure.

References

• Learning Discrete Distributions by Dequantization by Emiel Hoogeboom et al, 2020
• Categorical Normalizing Flows via Continuous Transformations by Lippe and Gavves, UVA, ICLR 2021

dequantization-for-categorical-data-categorical-nfs-via-continuous-transformations-a-paper-review