Please find the original discussion here

• Yann LeCun - Jun, 2021
• Steven Pinker - Jun, 2021
• Andre Ye - Jul, 2020
• Gary Marcus - Jul, 2021
• François Chollet - Oct, 2021
• Laura Ruis - Nov, 2021

Objective

The objective of this post is to consummate the views of Yann LeCun, Gary Marcus and François Chollet on the fundamentals of Deep Learning Systems. Also, I have added quotes from Laura Ruis’ explanation and implementation of the paper Learning in High Dimension Always Amounts to Extrapolation by Randall Balestriero, J´erome Pesenti, and Yann LeCun.

Introduction

Deep Learning often caused me an uncomfortable feeling because of its foundational principle of Gradients(descent/ascent or the backprop algorithm). I am not a scholarly being and often lack the articulation to convey my thoughts mainly the discomfort when it comes to the underlying learning process of deep learning models. My posts often made a rendition of my discomfort by portraying through various aspects like

1. Lack of explainability, trustworthiness
2. Inability to identify inductive biases
3. Poor causal conditions,
4. Not having a human-like efficiency or
5. Substandard knowledge representation

I am just collating and reproducing the discussion that happened in twitter for everyone’s benefit.

PS: It is a bit difficult to follow the conversation as twitter posts.

Steven Pinker - Jun 29, 2021

Excellent explanation of why neural networks work (when they do) & why they often don’t. (Common knowledge w/in cog sci but seldom stated so clearly.) You Don’t Understand Neural Networks til You Understand the Universal Approximation Theorem by Andre Ye

You Don’t Understand Neural Networks Until You Understand the Universal Approximation Theorem by Andre Ye, Jul 1, 2020

Yann LeCun - Replying to Steven Pinker

Jun 29, 2021

This is another piece that basically says “deep learning is not as impressive as you think because it’s mere interpolation resulting from glorified curve fitting”. But in high dimension, there is no such thing as interpolation. In high dimension, everything is extrapolation.

Felix Hill

Jun 30, 2021

Why do you think this criticism is so popular, even among clever folk, if it’s essentially vacuous?

Yann LeCun

Jun 30, 2021

Good question. It’s often voiced by people who are pushing for particular approaches to AI that do not involve learning, e.g. symbols! logic! causality! explainability! knowledge representation! prior structure! Or people with nativist visions of intelligence.

Minh Le

Jun 30, 2021

Yet NN does behave like the limited Taylor Series approximation mentioned in this piece. Just pass random noise to an ImageNet-trained convnet and it will go haywire.

Yann LeCun

Jun 30, 2021

It won’t go haywire. It will output one of the 1000 categories of ImageNet, because that’s exactly what it has been trained to do. If you don’t force the net to produce one of the categories during training (e.g. by training on “none of the above” samples), it won’t go “haywire”.

Mastering-openscad

Jun 30, 2021

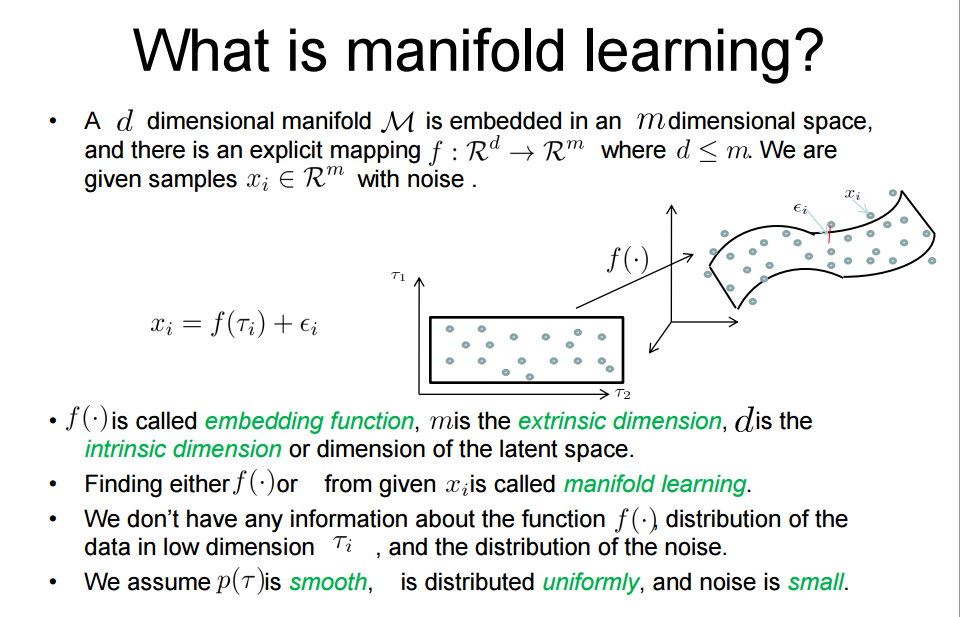
technically, most natural data lies on a low dimensional manifold. It does not really matter if it is delivered as high-dimensional vectors… so, possibly still “interpolation”.

• Refer: Manifold learning: How should this method be interpreted?

Yann LeCun

Jun 30, 2021

Yes, most natural data has strong regularities, which may manifest itself by a non-linear manifold in the ambient space.

But identifying this manifold (e.g. learning a function that can tell you if you are on it or not) is a much harder problem than mere “curve fitting”.

What is Ambient Space

The dimension $d$ of the Gaussian is called the ambient dimension. The ambient dimension of the data is the number of dimensions we use to represent it. If we take the well known MNIST datasetas an example, the ambient dimension that is often used is the number of pixels $d= 28 \times 28 = 784$

- Laura Ruis, 2021

Andrew Steckley

30 Jun, 2021

Can u elaborate? In this UAT context, interp(vs extrap.) really just refers to regions within the space that are sufficiently dense enough to approx. the hidden function. And particularly wrt those dimensions that most govern the fn. That seems valid in hi dims too, no?

Yann LeCun

Jun 30, 2021

In high-dimensional spaces, no data is dense.

Bernardo Subercaseaux

Jun 20, 2021

Just playing devil’s advocate, but it isn’t k-NearestNeighbors (as well as other non-DL algorithms) always interpolation? I don’t have anything against glorified curve fitting in any case, I believe that’s all there is behind intelligence

Thomas G. Dietterich

Jun 29, 2021

As the dimension increases, the distance between any pair of points grows rapidly. The “nearest neighbor” in high dimensions is far way (with high probability)

Gary Marcus - Replying to Yann LeCun

Jul 4, 2021

No, @ylecun, high dimensionality doesn’t erase the critical distinction between interpolation & extrapolation.

Thread on this below, because only way forward for ML is to confront it directly.

To deny it would invite yet another decade of AI we can’t trust.

Gary Marcus

Jul 4, 2021

Let’s start with a simple example drawn from my 2001 book The Algebraic Mind, that anyone can try at home:

The Algebraic Mind - Integrating Connectionism and Cognitive Science

Gary Marcus

Jul 4, 2021

Train a basic multilayer perceptron on the identity function (ie mulltiplying the input times one) on a random subset of 10% of the the even numbers, from 2 to 1024, representing each number as a standard distributed representation of nodes encoding binary digits.

Gary Marcus

Jul 4, 2021

What you will find is that the network can often interpolate – generalizing from some set of even numbers to some other even numbers, but never reliably extrapolate to odd numbers, which lie outside the trading space.

Gary Marcus

Jul 4, 2021

There are any number fo workarounds to this.

But adding more dimensions per se does not help. Try for example to train the neural net on a randomlly drawn subset of the even numbers up to 2^16.Or 2^256, if you like.

Gary Marcus

Jul 4, 2021

Again, you will find some interpolation to withheld even numbers, but you still won’t get reliable extrapolation to odd numbers.

Gary Marcus

Jul 4, 2021

Systems like GPT-3 behave erratically, I conjecture, precisely because some test items are far in n-dimensional space from the training set, hence not solvable with interpolation; failures occur when extrapolation is required.

Gary Marcus

Jul 4, 2021

*Because the training set is not publicly available, it is not possible to test this conjecture directly. @eleuther or @huggingface might want to give it a shot with their GPT+like models. (8/9) cc @LakeBrenden who has valuable, related evidence.

Gary Marcus

Jul 4, 2021

The good news is that Yoshua Bengio has begun to recognize the foundational nature of this challenge of extrapolation (he calls it “out of distribution generalization:).

The rest of the field would do well to follow his lead.

François Chollet

Oct 19, 2021

A common beginner mistake is to misunderstand the meaning of the term “interpolation” in machine learning.

Let’s take a look ⬇️⬇️⬇️

François Chollet

Oct 19, 2021

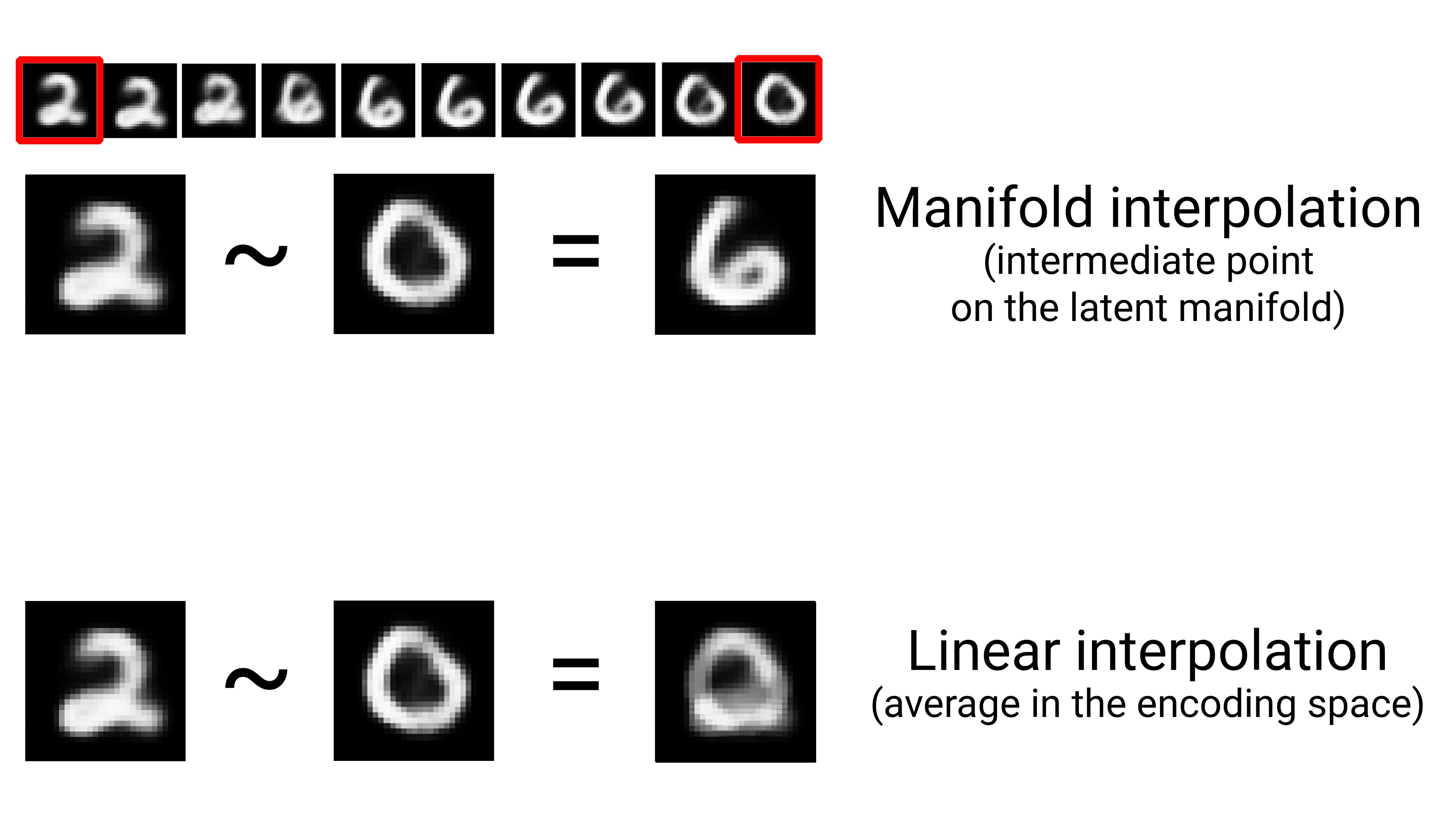
Some people think it always refers to linear interpolation – for instance, interpolating images in pixel space. In reality, it means interpolating on a learned approximation of the latent manifold of the data. That’s a very different beast!

François Chollet

Oct 19, 2021

Let’s start with a very basic example. Consider MNIST digits. Linearly interpolating between 2 MNIST samples does not produce a MNIST sample, but blurry images: pixel space is not linearly interpolative for digits!

François Chollet

Oct 19, 2021

However, if you interpolate between two digits on the latent manifold of the MNIST data, the mid-point between two digits still lies on the manifold of the data, i.e. it’s still a plausible digit.

François Chollet

Oct 19, 2021

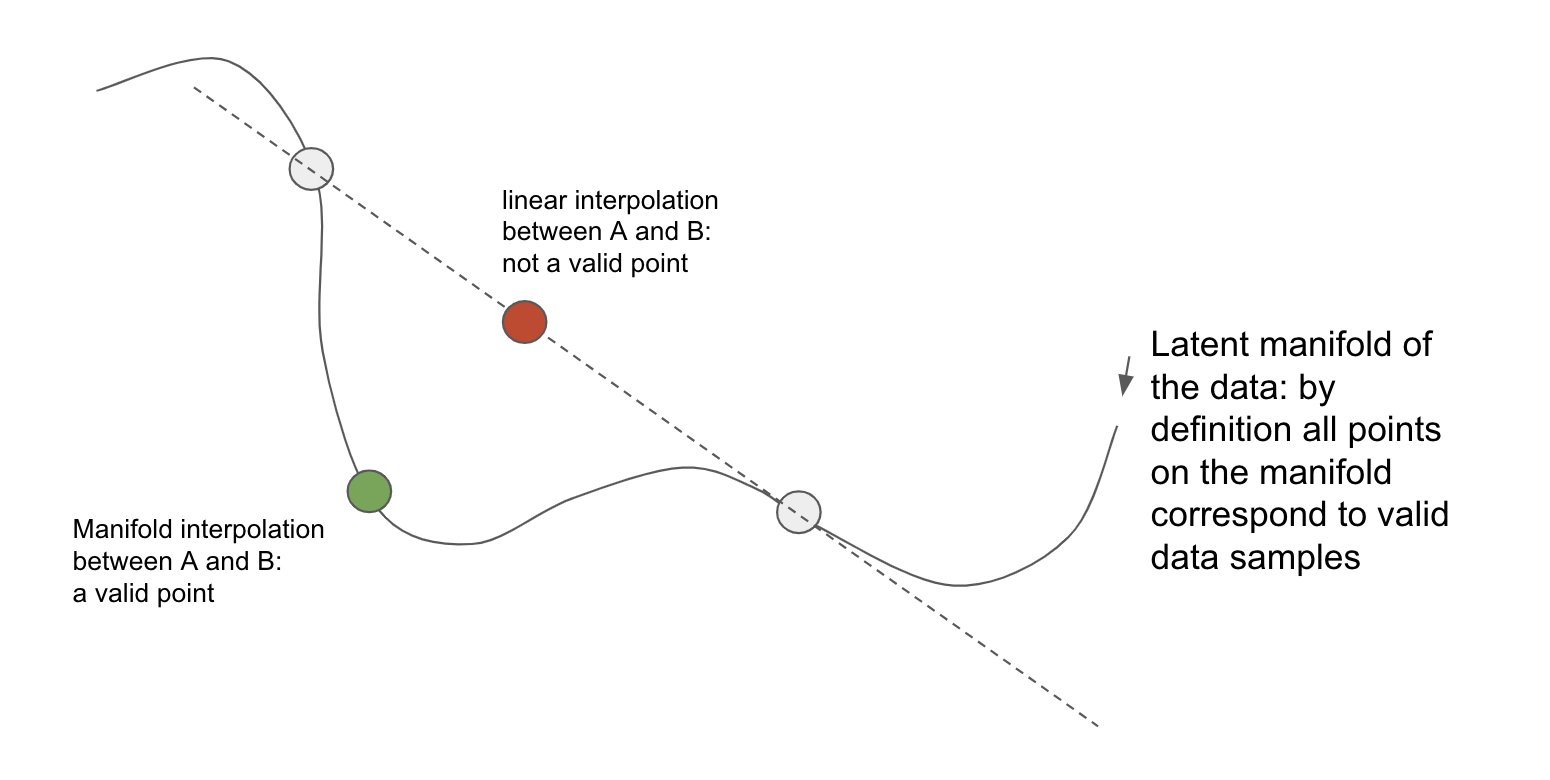
Here’s a very simple way to visualize what’s going on, in the trivial case of a 2D encoding space and a 1D latent manifold. For typical ML problems, the encoding space has millions of dimensions and the latent manifold has 2D-1000D (could be anything really).

François Chollet

Oct 19, 2021

But wait, what does that really mean? What’s a “manifold”? What does “latent” mean? How do you learn to interpolate on a latent manifold?

François Chollet

Oct 19, 2021

Let’s dive deeper. But first: if you want to understand these ideas in-depth in a better format than a Twitter thread, grab your copy of Deep Learning with Python, 2nd edition, and read chapter 5 (“fundamentals of ML”). It covers all of this in detail.

Deep Learning with Python, Second Edition

François Chollet

Oct 19, 2021

Ok, so, consider MNIST digits, 28x28 black & white images. You could say the “encoding space” of MNIST has 28 * 28 = 784 dimensions. But does that mean MNIST digits represent “high-dimensional” data?

François Chollet

Oct 19, 2021

Not quite! The dimensionality of the encoding space is an entirely artificial measure that only reflects how you choose to encode the data – it has nothing to do with the intrinsic complexity of the data.

François Chollet

Oct 19, 2021

For instance, if you take a set of different numbers between 0 and 1, print them on sheets of paper, then take 2000x2000 RGB pictures of those papers, you end up with a dataset with 12M dimensions. But in reality your data is scalar, i.e. 1-dimensional.

How? $$2000 \times 2000 \times 3 \ Channels = 12,000,000 = 12M$$

François Chollet

Oct 19, 2021

You can always add (and usually remove) encoding dimensions without changing the data, simply by picking a different encoding scheme. That is, until you hit the “intrinsic dimensionality” of the data (past which you would be destroying information).

François Chollet

Oct 19, 2021

For MNIST, for instance, very few random grids of 28x28 pixels form a valid digit. Valid digits occupy a tiny, microscopic subspace within the encoding space. Like a grain of sand in a stadium. You call it the “latent space”. This is broadly true for all forms of data.

François Chollet

Oct 19, 2021

Further, the valid digits aren’t sprinkled at random within the encoding space. The latent space is highly structured. So structured, in fact, that for many problems it is continuous.

François Chollet

Oct 19, 2021

This just means that for any two samples, you can slowly morph one sample into the other without “stepping out” of the latent space.

François Chollet

Oct 19, 2021

For instance, this is true for digits. This is also true for human faces. For tree leaves. For cats. For dogs. For the sounds of the human voice. It’s even true for sufficiently structured discrete symbolic spaces, like human language!

(face grid image by the awesome @dribnet)

François Chollet

Oct 19, 2021

The fact that this property (latent space = very small subspace + continuous & structured) applies to so many problems is called the manifold hypothesis. This concept is central to understanding the nature of generalization in ML.

François Chollet

Oct 19, 2021

The manifold hypothesis posits that for many problems, your data samples lie on a low-dimensional manifold embedded in the original encoding space.

François Chollet

Oct 19, 2021

A “manifold” is simply a lower-dimensional subspace of some parent space that is locally similar to a linear (Euclidian) space. (i.e. it is continuous and smooth). Like a curved line within a 3D space.

François Chollet

Oct 19, 2021

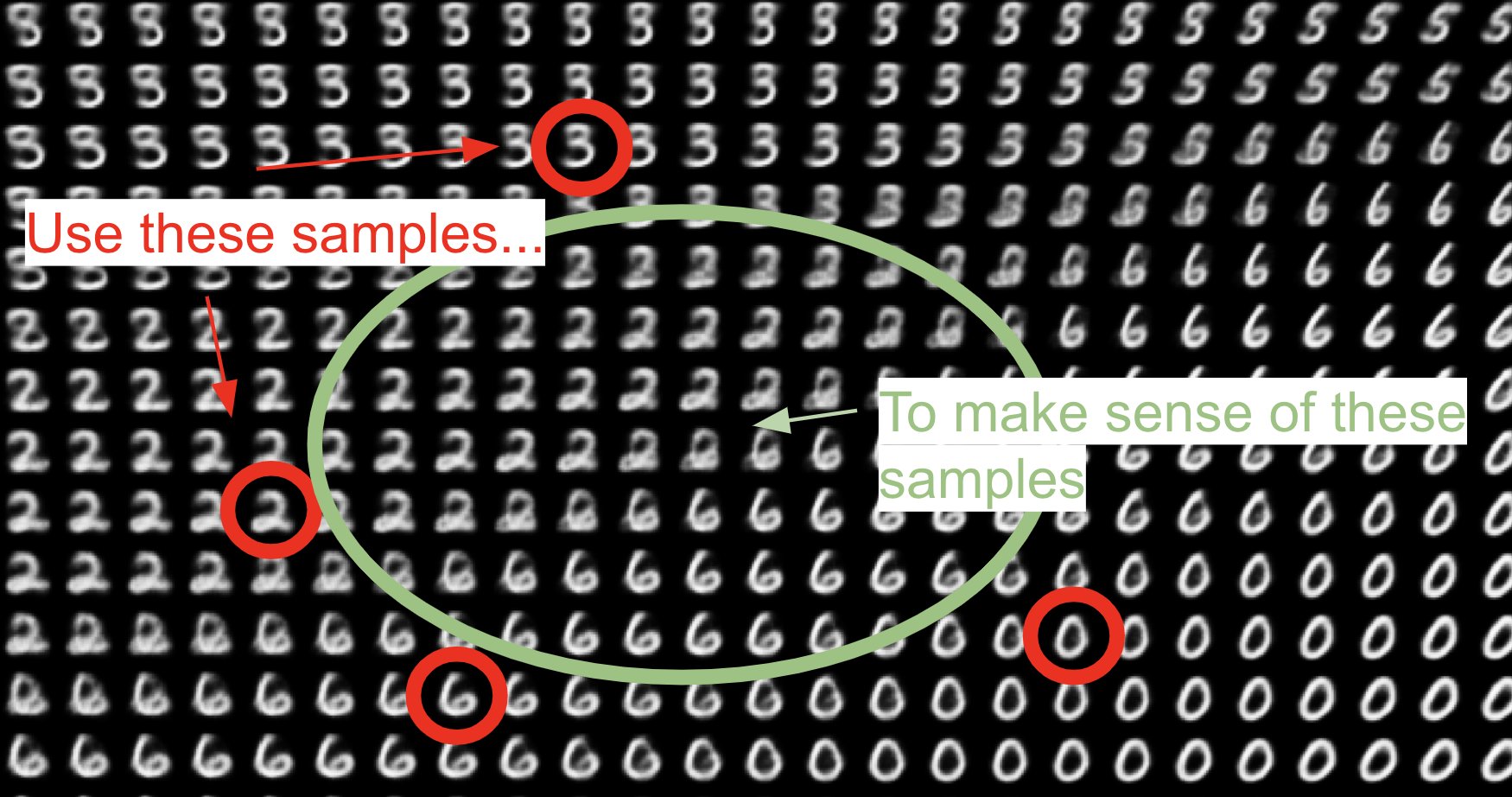
When you’re dealing with data that lies on a manifold, you can use interpolation to generalize to samples you’ve never seen before. You do this by using a small subset of the latent space to fit a curve that approximately matches the latent space.

François Chollet

Oct 19, 2021

Once you have such a curve, you can walk on the curve to make sense of samples you’ve never seen before (that are interpolated from samples you have seen). This is how a GAN can generate faces that weren’t in the training data, or how a MNIST classifier can recognize new digits

François Chollet

Oct 19, 2021

If you’re in a high-dimensional encoding space, this curve is, of course, a high-dimensional curve. But that’s because it needs to deal with the encoding space, not because the problem is intrinsically high-dimensional (as mentioned earlier).

François Chollet

Oct 19, 2021

Now, how do you learn such a curve? That’s where deep learning comes in.

François Chollet

Oct 20, 2021

But by this point this thread is LONG and the Keras team sync starts in 30s, so I refer you to DLwP, chapter 5 for how DL models and gradient descent are an awesome way to achieve generalization via interpolation on the latent manifold.

François Chollet

Oct 19, 2021

I’m back, just wanted to add one important note to conclude the thread: deep learning models are basically big curves fitted via gradient, that approximate the latent manifold of a dataset. The quality of this approximation determines how well the model will generalize.

François Chollet

Oct 19, 2021

The ideal model literally just encodes the latent space – it would be able to perfectly generalize to any new sample. An imperfect model will partially deviate from the latent space, leading to possible errors.

François Chollet

Oct 19, 2021

Being able to fit a curve that approximates the latent space relies critically on two factors:

1. The structure of the latent space itself! (a property of the data, not of your model)
2. The availability of a “sufficiently dense” sampling of the latent manifold, i.e. enough data

Baranay and Furedi - Theorem 1

• Given a d-dimentional dataset $X \in {x_1, \cdots, x_N }$ with independent identical distributed samples $x_n \thicksim \mathcal{N}(0, \mathbb{I}_d)$
• For all $n_i$, the probability that a new sample $x \thicksim \mathcal{N}(0, \mathbb{I}_d)$ is in interpolation regime

$$\lim_{d \rightarrow \inf} p(x \in Hull(X))$$ $$where$$ $$1 \ if \ N > \frac{2^{d/2}}{d}$$ $$0 \ if \ N < \frac{2^{d/2}}{d}$$

• The probability that aa new sample lies in the convex hull of $N$ samples tends to one for increasiing dimensions if $N > \frac{2^{d/2}}{d}$
• If $N$ is smaller, it tends to 0
• Implies, We need to exponentially increase the number of datapoints $N$ for increasing $d$

We need more observatoins if we want to be in the hull for higher dimensions

François Chollet

Oct 19, 2021

You cannot generalize in this way to a problem where the manifold hypothesis does not apply (i.e. a true discrete problem, like finding prime numbers).

François Chollet

Oct 19, 2021

In this case, there is no latent manifold to fit to, which means that your curve (i.e. deep learning model) will simply memorize the data – interpolated points on the curve will be meaningless. Your model will be a very inefficient hashtable that embeds your discrete space.

François Chollet

Oct 19, 2021

The second point – training data density – is equally important. You will naturally only be able to train on a very space sampling of the encoding space, but you need to densely cover the latent space.

François Chollet

Oct 19, 2021

It’s only with a sufficiently dense sampling of the latent manifold that it becomes possible to make sense of new inputs by interpolating between past training inputs without having to leverage additional priors.

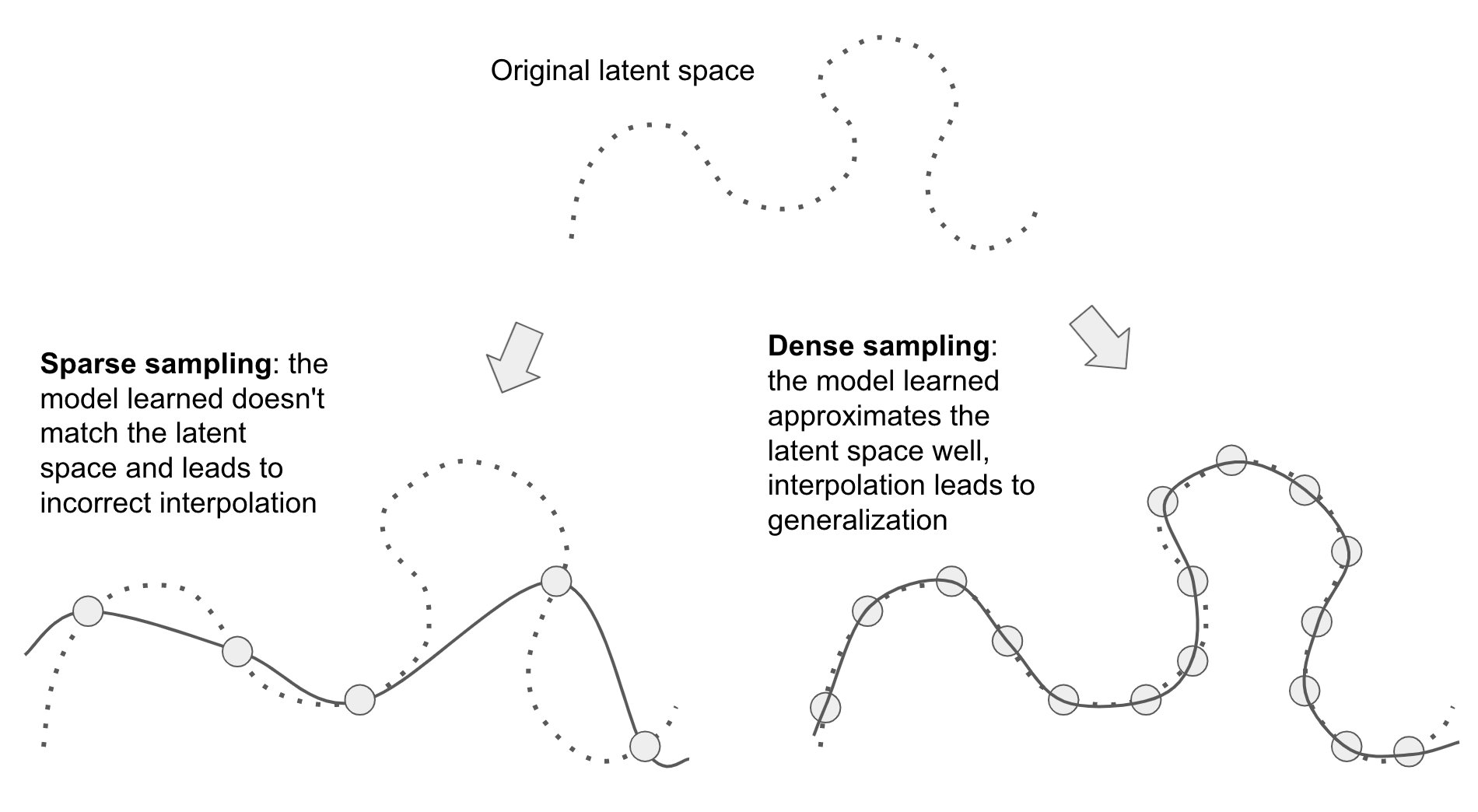
François Chollet

Oct 19, 2021

The practical implication is that the best way to improve a deep learning model is to get more data or better data (overly noisy / inaccurate data will hurt generalization). A denser coverage of the latent manifold leads a model that generalizes better.

David Piccard

Oct 20, 2021

The entire thread makes the assumption there is no disconnectedness. This is not the case for images, eg, face with glasses vs face without glasses. There is no continuous path from one to the other that only contains natural images.

Thomas G. Dietterich

Oct 19, 2021

Confusion avoidance: There is another use of “interpolation” in ML. A model interpolates the training data if it exactly fits the data (loss = 0). I guess this is by analogy with interpolating splines:

Thomas G. Dietterich

Oct 19, 2021

Your overall point is that “interpolation” requires specifying a representation (manifold + distance) over which the computation is performed. One CAN interpolate in the image space, and one can interpolate in a fitted manifold. The latter works much better, of course.

References

• Learning in High Dimension Always Amounts to Extrapolation by LeCun et al, 2021