This is our $4^{th}$ post on Graph Neural Networks and $2^{nd}$ on Message Passing Neural Networks(MPNN), In our earlier post we studied the SMILES representation of the molecular structure and a scheme for converting the molecular structures to graph representations. Further, we created tensors representing the atomic properties, bond properties, and pairing information. In this post, we shall understand the problem statement, quantum chemical properties of the molecules, and the MPNN algorithm to their finer detail. Previous posts can be referred to here.

• Introduction to Graph Neural Networks
• Graph Convolution Network - A Practical Implementation of Vertex Classifier and it’s Mathematical Basis
• Atoms and Bonds - Graph Representation of Molecular Data For Drug Detection

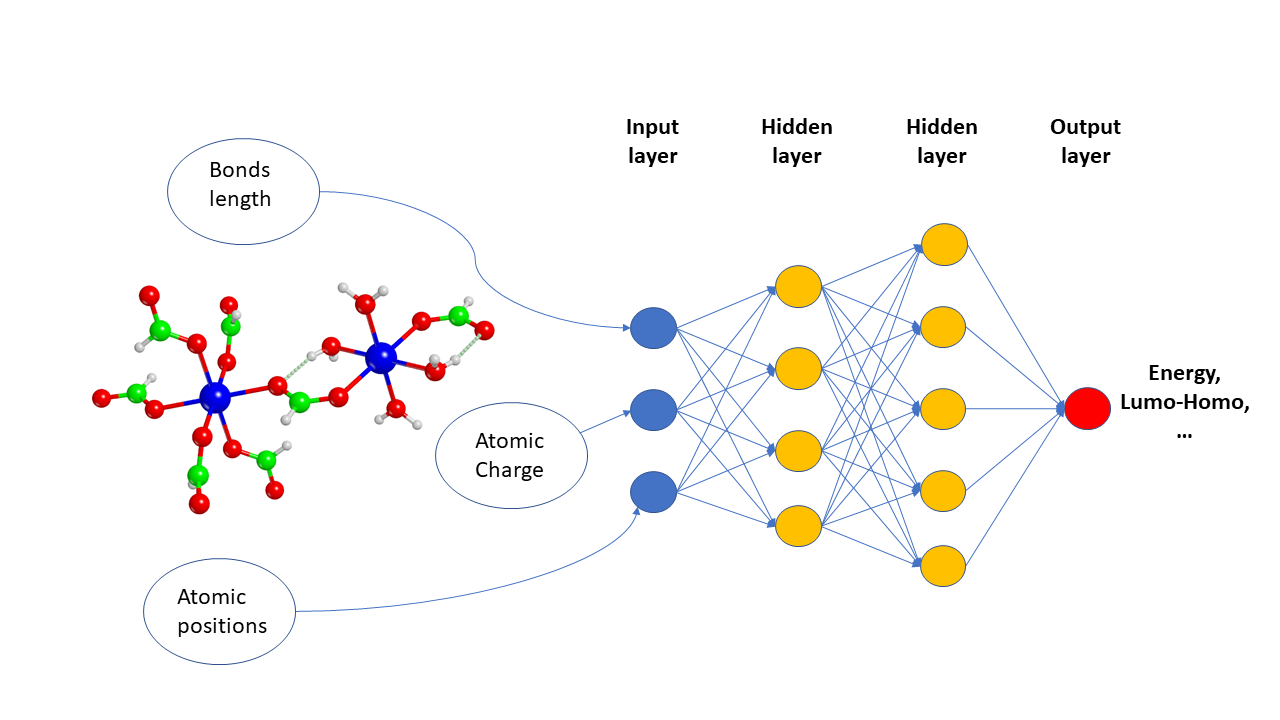
This post is a walkthrough of Gilmer, Dahl et al’s seminal paper Neural Message Passing for Quantum Chemistry. In my earlier post, I have covered the mathematical foundation of MPNN. This post covers few critical sections of their scholarly work in an unscholarly manner.

Objective

The key objective of this post is to understand the complexity involved in understanding molecular dynamics of chemical compounds, their properties in detail and study deep learning-based schemes for predicting quantum properties of them. In that process, we shall learn the following,

• Density functional theory (DFT)
• QM9 Dataset
• Quantum chemical properties of molecules
• Input representation of quantum chemical properties
• Message passing neural network design
  • Message functions
  • Edge Networks
  • Pair Messages
  • Readout Functions

Introduction

In computational chemistry(and physics), properties of electron structures of a certain class of atoms and molecules are modeled using Density Functional Theory(DFT). DFT scheme is a quantum mechanical modeling method, first appeared during the early 70s and constantly evolved/refined through the years. They are state-of-the-art, one of kind modeling techniques that model the exchange and correlation interaction of the atoms and molecules and their energy states.

The DFT scheme is a compute-intensive one due to the involvement of large-scale quantum mechanical calculations that result in the generation of data at a very high rate. The dataset(QM9, publicly available) we use has 134k molecules with 17 properties for each molecule. These features are approximated via 17 regression tasks. The 17 features cover the geometric, energetic, electronic, and thermodynamic properties of the molecules. The efficacy of the models are evaluated against 2 parameters,

1. DFT Error: The estimated average error of the DFT approximation to nature
2. Chemical Accuracy: Target error that has been established by the chemistry community, measured in $eV$.

The objective is to achieve chemical accuracy and DFT error for all 13 target properties that determine the magnetic interaction between two atoms in a molecule.

Quantum Machine 9(QM9)

Quantum machine 9 datasets consist of the following chemical compounds

• Hydrogen
• Carbon(C)
• Oxygen(O)
• Nitrogen(N)
• Fluorine(F) and
• 9 Heavy Non-Hydrogen Atoms

Each molecule has the following properties,

• tag: gdb9; string constant to ease extraction via grep
• index: Consecutive, 1-based integer identifier of molecule
• A (GHz): Rotational constant A
• B (GHz): Rotational constant B
• C (GHz): Rotational constant C
• mu (Debye): Dipole moment
• $\alpha$ (Bohr^3): Isotropic polarizability
• homo (Hartree): Energy of Highest occupied molecular orbital (HOMO)
• lumo (Hartree): Energy of Lowest occupied molecular orbital (LUMO)
• gap (Hartree): Gap, the difference between LUMO and HOMO
• $r^2$ (Bohr^2): Electronic spatial extent
• $zp_{ve}$ (Hartree): Zero-point vibrational energy
• $U_0$ (Hartree): Internal energy at 0 K
• U (Hartree): Internal energy at 298.15 K
• H (Hartree): Enthalpy at 298.15 K
• G (Hartree): Free energy at 298.15 K
• $C_v$ (cal/(mol K)): Heat capacity at 298.15 K

• Image Credit: Pinheiro et al had done an in-depth exploratory analysis on QM9 properties

Quantum Properties Elaborated

The properties discussed above can be grouped into 4 categories as follows,

• By the measure of the energy required to break the molecule
• By the vibrations of the molecule
• By the state of the electrons in the molecule
• By the spatial distribution of electrons in the molecule

Measure of Energy

The energy required to break a molecule at various pressure and the temperature level is critical for any reaction. There are 4 properties

• $U_0$ ($eV$, Hartree): Atomization energy at 0 K, Atomization energy is the energy required to break up the molecule into all of its constituents.
• U ($eV$, Hartree): Atomization Energy at room temperature 298.15 K
• H ($eV$, Hartree): Enthalpy atomization at room temperature 298.15 K, Enthalpy means the constituents are held at a fixed pressure
• G ($eV$, Hartree): Free energy of atomization at 298.15 K, Free energy means the energy required for atomization when the temperature and pressure are fixed.

Vibration of Molecule

The fundamental vibrations of the molecule,

• $\omega_1$ ($cm^{-1}$): The highest fundamental vibrational frequency, at this frequency the molecule naturally oscillates.
• $zp_{ve}$ ($eV$): Zero-point vibrational energy. When the temperature is zero, quantum mechanical uncertainty implies that atoms vibrate.

State of the Electrons

Following are the properties that denote the state of the electrons in the molecule,

• $\epsilon_{HOMO}$ ($eV$): Energy of the highest occupied molecular orbital(HOMO). According to Pauli’s exclusion principle, no 2 electrons may occupy the same state and Quantum mechanics states that the allowed state that electrons can occupy in a molecule are discrete. Hence, electrons stack in states from lowest to highest energy levels.
• $\epsilon_{LUMO}$ ($eV$): Energy of the lowest unoccupied molecular orbital(LUMO)
• $\Delta_{\epsilon}$ ($eV$): The electron energy gap $\epsilon_{HOMO} - \epsilon_{LUMO}$. It is the lowest energy transition that can occur when an electron is excited from an occupied state to an unoccupied state. It also dictates the longest wavelength of light that the molecule can absorb.

Spatial Distribution of the Electrons

3 Measures of spatial distributions of electrons in the molecule,

• $R^2, (Bohr^2)$: Electronic spatial extent. It is the second moment of the charge distribution, $\rho(r)$ $$R^2 = \int drr^2 \rho(r)$$
• $\mu (Debye)$: The norm of the dipole moment. It approximates the electric field far from a molecule.

• $\alpha$, Bohr^3: The norm of static polarizability. It measures the extent to which a molecule can spontaneously incur a dipole moment in response to an external field. It turns to a degree to which Van der Waals interactions play a role in the dynamics of the medium.

MPNN

Conventional Deep Learning architectures pre-process the input into a tabular or sequence format before feeding it into the network. This process is inefficient and loses information when it comes to graph data, i.e adjacency sparse matrix of graph information far from the actual representation.

Introduction from the previous post, refer here

The molecules of materials can be represented as Graph structures where atoms are the vertices and bonds are the edges. A MPNN architecture takes an undirected graph with node features $x_v$ and bond feature $e_{vw}$ as input. With these features as input, MPNN operates at 2 phases

• Message Passing Phase and
• Readout Phase

In the message-passing phase, information is propagated across the graph to build the neural representation of the graph, and the readout phase is when the predictions are made. Wrt molecular graphs, the goal is to predict the quantum molecular properties based on the topology of the molecular graph.

For each vertex $v$, there is an associated hidden state and their messages at every time step $t$. $$\Large m_v^{t+1} = \sum_{w \in N(v)} M_t(h_v^t, h_w^t, e_{vw}) \tag{1. Messages associated to the vertex }$$ $$\Large h_v^{t+1} = U_t(h_v^t, m_v^{t+1}) \tag{2. Hidden state for the vertex}$$

Where,

• $e_{vw}$ is the edge feature
• $M_t$ is message functions
• $U_t$ is vertex update functions
• $N(v)$ us the neighbors of $v$ in the graph

In the readout phase, a readout function is applied to the final hidden states $h_v^T$ to makes the predictions, $$\Large \hat y = R({h_v^T|v \in G}) \tag{3. Predicted Quantum Properties}$$

Where $G$ is the molecular graph.

It would be possible to learn edge features using an MPNN by introducing hidden states for all edges in the graph $h_{e_{vw}}^t$ and updating them as was done with equations 1 and 2.

Message Functions

MPNN implementation operates on directed graphs where the edge becomes both incoming and outgoing edge with the same label. The core of MPNN architecture is to figure outright

• Message functions,
• Output functions and
• Appropriate input representation

Since we consider it as a directed graph, we have separate message channels for incoming and outgoing edges in which incoming message is the concatenation of outgoing and incoming.

Input representation

• $x_v$: Set of feature vectors for the nodes of graph $G$.
• $A$: An adjacency matrix with vectors indicating different bonds in the molecule and pairwise spatial distance between atoms.

Message Functions

• Message function assumes discrete edge labels of size $k$
• A GRU layer is used for weight tying at each time step $t$, Refer Alexander Kensert’s class MessagePassing here

$$\Large m_{wv} = f(h_w^t, h_v^t, e_{vw}) \tag{4. Pair Message}$$ Where,

• $m_{wv}$ is the message from node $w$ to $v$

Compute Complexity

A Single step of the message passing phase for a dense graph requires $O(n^2d^2)$ floating point multiplications lead to computationally expensive. Where $n$ is the number of nodes and $d$ is the dimension of the internal hidden representation. $d \rightarrow \ node \ embeddings$ further optimized to $O(n^2\frac{d^2}{k})$, where k temporary embeddings of each node are then mixed together as follows $$\left(h_v^{t, 1}, h_v^{t, 2}, \cdots, h_v^{t, k}\right) = g \left(\tilde h_v^{t, 1}, \tilde h_v^{t, 2}, \cdots, \tilde h_v^{t, k}\right) \tag{5. Mixture of Temporary Embeddings}$$

• $g \rightarrow$ a neural network shared across all nodes in the graphs

Evaluation Metric (MAE)

The efficacy of the model is measured using the ratio of mean absolute error (MAE) with the provided estimate of chemical accuracy for that target. MAE of the model is calculated as follows $$\Large MAE = (Error Ratio) \times (Chemical Accuracy) \tag{6. Evaluation Metric}$$

Conclusion

In this post, we revisited the concepts of chemical compounds that we have studied during our school days. It is refreshing and nostalgic when we look at something we possess but have forgotten for years. Further, we are evolving from object detection and named entity recognition to complex problems of nature. GNN for drug discovery is a significant breakthrough among the deep learning fraternity, this research work inspires us to see everything as nodes and edges. However, compute the complexity of MPNN comes as a hurdle for exploring further. We are still in the nascent stage of graph-based deep learning algorithms and the bests are yet to come.

I thank Alexandar Kensert for implementing and publishing MPNN using Tensorflow, It simplified the understanding process and inspired me to write this post. Without his work, It would have been quite challenging to realize the class MessagePassing and the class PartitionPadding modules of MPNN architecture. I believe I will be writing one more post on GNNs as a conclusion note, until then adios amigos!

References

• Neural Message Passing for Quantum Chemistry by Gilmer, Dahl el al from DeepMind 2017
• QM9 Dataset from Quantum Machine
• Density functional theory for beginners by James Coover
• Density functional theory from Wikipedia
• Message-passing neural network for molecular property prediction by Alexandar Kensar, 2021
• How do Graph Neural Networks Work? by Madeline Schiappa, 2019
• Quantum Machine 9 - QM9 by No Sound, 2019
• Machine Learning Prediction of Nine Molecular Properties Based on the SMILES Representation of the QM9 Quantum-Chemistry Dataset by Pinheiro et al, 2020
• GNN Papers from Natural Language Processing Lab at Tsinghua University
• Deep Learning for Molecules and Materials by Andrwo White, 2021
• Predicting Molecular Activity Using Deep Learning in TensorFlow by Cathy Qian, 2018
• Machine Learning on Graphs (8/31 – 9/3) by Alejandro Ribeiro, UPenn, 2020