In this post, we shall study 8 different flavors of UTSMs by using statsmodels package. This post is an introductory guide to use statsmodel package where I focussed more towards the coding aspects rather than the mathematical foundation of the models studied. This is the 4th post on the Time Series Analysis where we studied Structural Time Series through GAMs, Please refer here

• Trend, Features of Structural Time Series, Mathematical Intuition Behind Trend Analysis for STS
• Fourier Series as a Function of Approximation for Seasonality Modeling - Exploring Facebook Prophet’s Architecture
• Structural Time Series Models, Why We Call It Structural? A Bayesian Scheme For Time Series Forecasting
• Is Covid Crisis Lead to Prosperity - Causal Inference from a Counterfactual World Using Facebook Prophet

Objective

The objective of this post is to do hands-on coding of univariate time series models for forecasting problems. In this process, we will be covering the following topics

• Yahoo Finance APIs to get stock market data
• Auto Regressive models, Moving Averages and Integrated models
• Seasonality factors and exogenous data

Introduction

Univariate analysis is a qualitative analysis of single variable changing at certain reference dimension. When the reference dimension is time, we call it univariate time series analysis - Which is the simplest of all time series analysis modeling schemes. When there is only one variable to account, the output or the predicted value is linearly depend on its own previous values. Once they are combined with moving averages, we form a special cases of linear dependents like ARMA to ARIMA etc. Further we can extend this by adding seasonality(SARMA) and exogenous data(SARIMAX) for better outcomes.

In this post, we acquire the stock market day close data of 4 Fast Moving Consumer Goods(FMCG) manufacturers and build our time series models. Our approach is to build a simplest model and improve it step by step by adding various schemes to it. As I mentioned earlier, this is more focussed on statsmodel package usage for time series forecasting rather than studying the nuances of the algorithm behind - an unscholarly attempt for time series.

Data

Using yfinance package, we download stock market data of

• Unilever, India
• Procter and Gamble, India
• Nestle, India and
• Diageo India

from 1st April, 2020 to 18th August, 2021. We then split the data by 80/20 ratio for train and test. Note, split happens sequentially rather than random choices to ensure the data is Independent and Identically Distributed to avoid leakage or interpolation of trend.

START_DATE = "2020-04-01"
END_DATE = "2021-08-18"
TRAIN_TEST_SPLIT = 0.8

PREDICTION_START_DATE = "2021-05-10"
PREDICTION_END_DATE = "2021-08-18"

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

import warnings
warnings.filterwarnings("ignore")
sns.set()

warnings.filterwarnings('ignore', 'statsmodels.tsa.arima_model.ARMA',
                        FutureWarning)
warnings.filterwarnings('ignore', 'statsmodels.tsa.arima_model.ARIMA',
                        FutureWarning)

Preprocessing

In this section, following activities are accomplished

• Using yfinance package data acquisition is done from NSE, India index for the tickers HINDUNILVR.NS, PGHH.NS, NESTLEIND.NS and MCDOWELL-N.NS
• We are analyzing the day close values, hence the rest of the observations are dropped
• By setting frequency as b, we consider business days of the week as discrete sequence
• Often data is not available for all weekdays due to holidays, imputing for those days are done using forward fill(ffill) scheme
• Train and test data sequence are split by 80/20 ratio

import yfinance
ticker_dict = {
    "Unilever": "HINDUNILVR.NS",
    "P&G": "PGHH.NS",
    "Nestle": "NESTLEIND.NS",
    "Diageo": "MCDOWELL-N.NS"
}
tickers = [value for key, value in ticker_dict.items()]

df = yfinance.download(" ".join(tickers), start = START_DATE,
    end = END_DATE, interval = "1d", group_by = 'ticker', auto_adjust = True, treads = True)
df_orig = df.copy()

# Day close and drop others
for key, value in ticker_dict.items():
    df[key]=df[value].Close[:]
    del df[value]

# Set frequency on business days of the week and Forward fill
df = df.asfreq('b').fillna(method='ffill')
df.shape

### Splitting the Data
train_length = int(len(df) * TRAIN_TEST_SPLIT)
df_train = df.iloc[:train_length]
df_test = df.iloc[train_length:]

[*********************100%***********************]  4 of 4 completed

Forecasting, Simple

Our forecasting section is broadly classified into 3

• Simple Forecast - Auto Regressive and Moving Averages
• Seasonal Forecast
• Integrated Forecast
• Forecast with Exogenous Variables

Simple Forecasting

Let us build 2 utility functions, one for training, predicting and storing the results for all the tickers in an efficient way and the second one for plotting the test and predicted data in a grid for easy comprehension.

ARIMA Util

• We use ARIMA API from the statsmodel package
• Train the model for the period starting 1st April, 2020 and ending 7th May, 2021
• Test for the period from 10th May, 2021 to 18th August, 2021

from statsmodels.tsa.arima_model import ARIMA

def arima_util(model_name, model_config, enforce_stationarity=False):

    model_output = {}
    for key in ticker_dict.keys():
        model_output[key] = {}

        fit_model = None
        predictions_df = None
        try:
            model = ARIMA(df_train[key], order=model_config)
            fit_model = model.fit()
            predictions_df = fit_model.predict(start=min(df_test.index), end=max(df_test.index))
            model_output[key]["isFit"] = True
        except Exception as e:
            print(f"Exception Occurred, while training {key} : ", e.__class__)
            print(e)
            model_output[key]["isFit"] = False

        model_output[key]["model"] = fit_model
        model_output[key]["predictions"] = predictions_df

    return model_output

def plt_predictions(df_actuals, model_predictions, title):
    fig, axs = plt.subplots(2, 2, figsize=(30, 20))
    fig.suptitle(title, size=32)
    row = 0
    col = 0
    for key in ticker_dict.keys():
        predictions = model_predictions[key]
        ax = axs[row, col]
        actuals = df_actuals[key]
        minn = actuals.min()
        maxx = actuals.max()
        ax.set_ylim(minn - minn * 0.1, maxx + maxx * 0.1)
        if predictions["isFit"]:
            ax.plot(predictions["predictions"], color="red")
        ax.plot(df_actuals[key], color="blue")
        ax.set_title(key, size=24)
        col += 1
        if(col == 2):
            row += 1
            col = 0

    plt.show()

The key parameter of ARIMA API is its order sequence, order sequence determines the selection of model for the training.

Auto Regressive

Auto regressive models are nothing but a simple linear regression done on the data over time. i.e In regular linear regression, outcome is correlated to the predictors whereas in AR models outcome is dependent on the previous values of its own. AR scheme is a stochastic process that has certain degree of uncertainty due to built-in randomness, makes it never a 100% accurate prediction.They are also Markovian in nature.

auto_regressive_models = arima_util("Auto Regressive", (1, 0, 0))
plt_predictions(df_test[PREDICTION_START_DATE:PREDICTION_END_DATE], auto_regressive_models, "Auto Regressive(AR)")

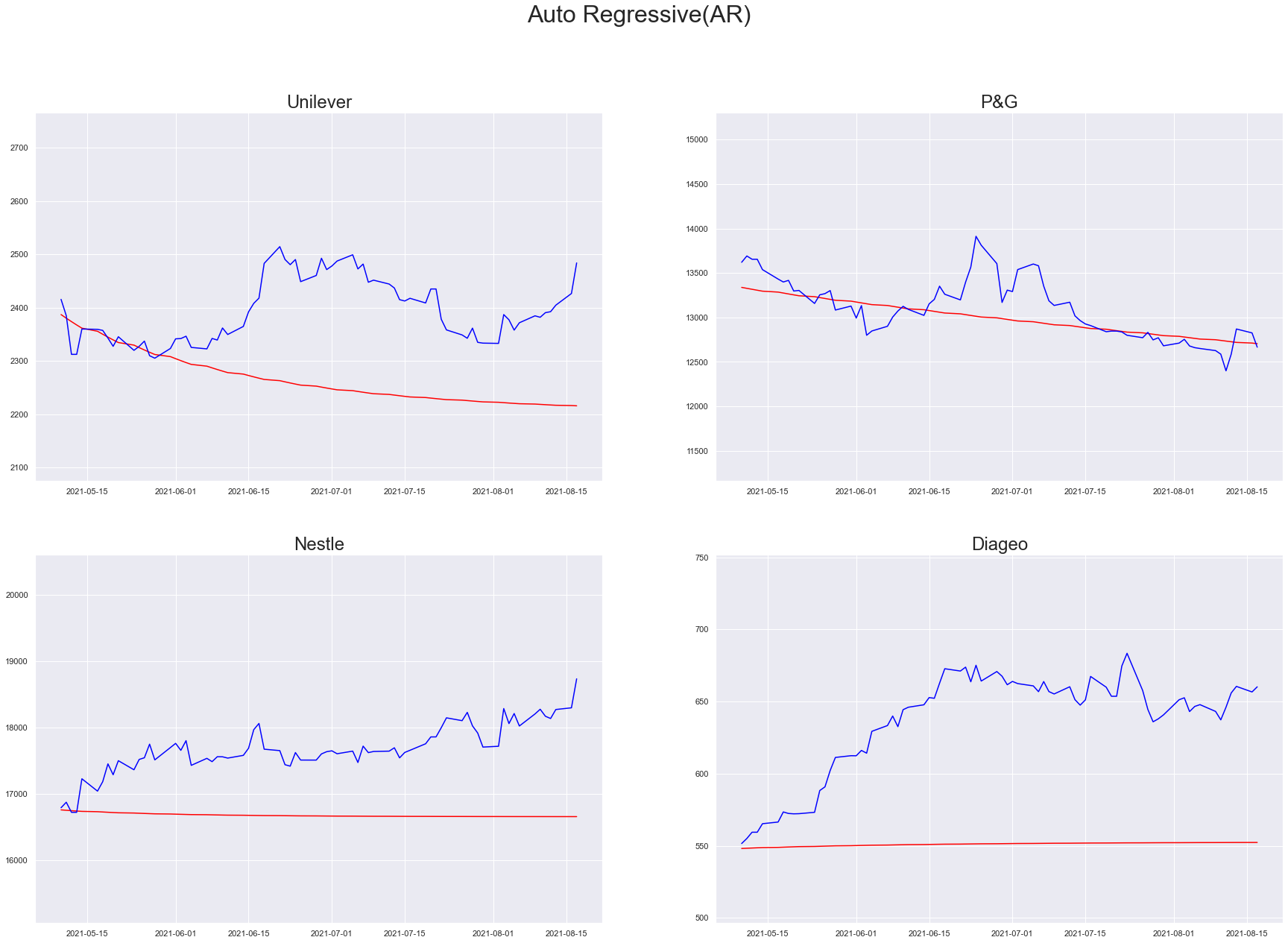
Moving Averages

A simple explanation for Moving Average is the next observation is the mean of past observations. The key difference between AR and MA is, AR part accomplishes the regression of its own lagged values(of the past) and MA accounts for short-run autocorrelation.

moving_averages_models = arima_util("Moving Averages(MA)", (0, 0, 1))
plt_predictions(df_test[PREDICTION_START_DATE:PREDICTION_END_DATE], moving_averages_models, "Moving Averages(MA)")

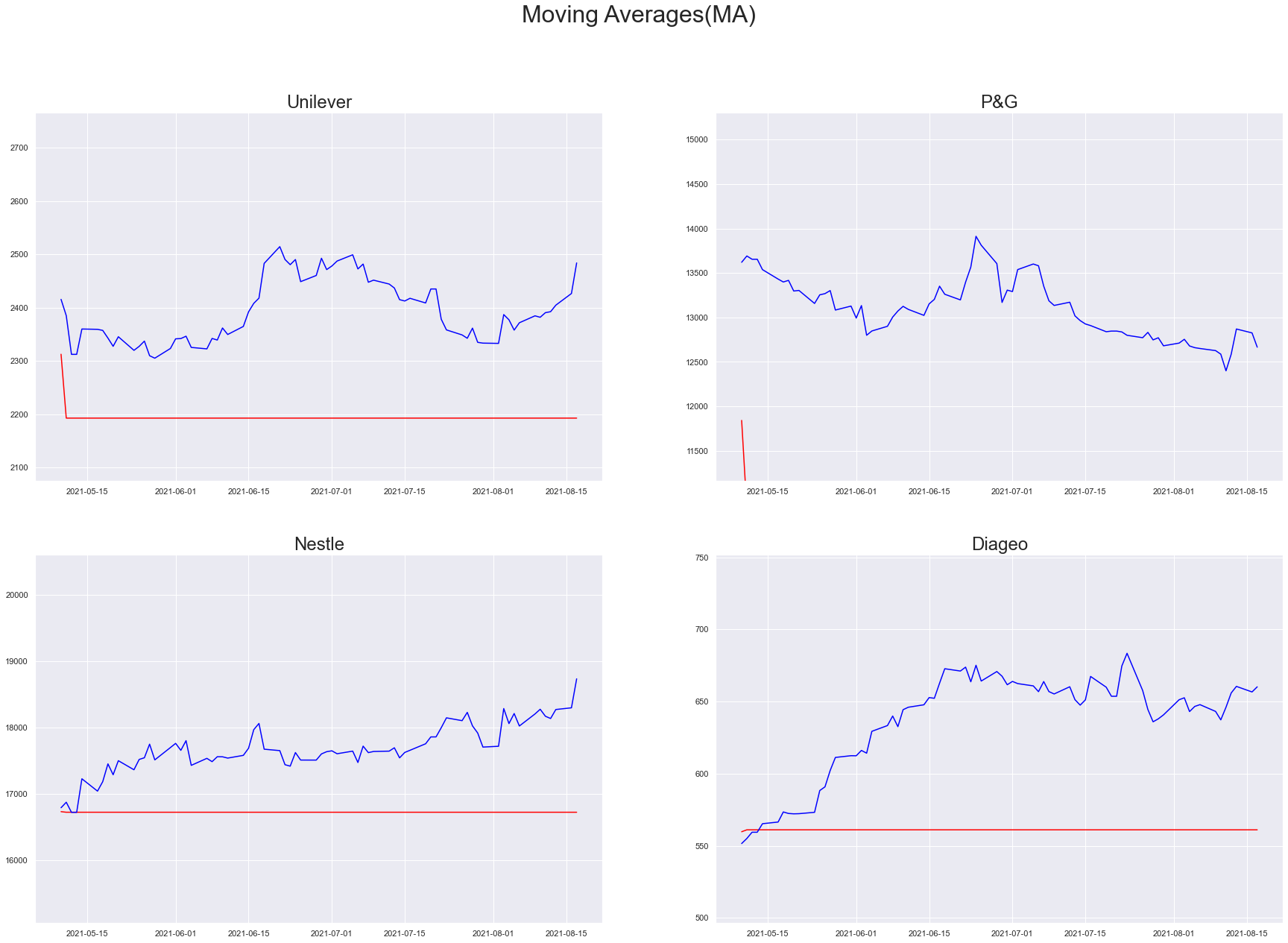
Auto Regressive - Moving Averages(ARMA)

We are studying two closely related ideas ARMA and ARIMA, the key difference between them is the process of differencing. ARMA models are stationary, stationarity in simple terms is a flat looking series with no trend and constant variance over time.

arma_models = arima_util("ARMA", (1, 0, 1))
plt_predictions(df_test[PREDICTION_START_DATE:PREDICTION_END_DATE], arma_models, "Auto Regressive Moving Averages(ARMA)")

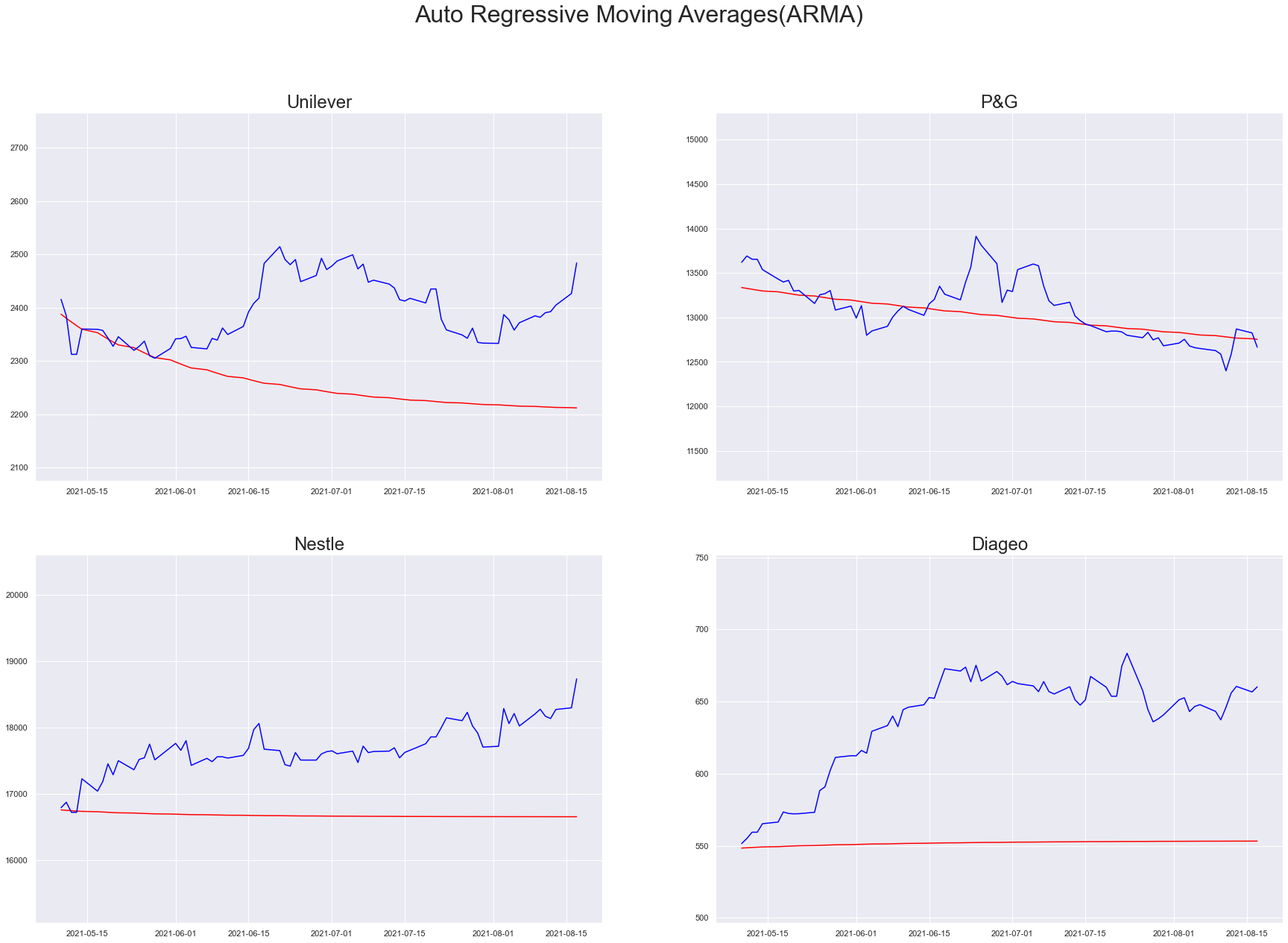
Integrated Model

ARIMA

The term I in ARIMA represents the measure of non-seasonal differences required to achieve stationarity . In ARMA modes we had the order (p, q) whereas in ARIMA we shall have the order (p, d, q).

arima_models = arima_util("ARIMA", (1, 1, 1))
plt_predictions(df_test[PREDICTION_START_DATE:PREDICTION_END_DATE], arma_models, "Auto Regressive Integrated Moving Averages(ARIMA)")

Seasonality

Time series data often exhibits seasonal variation and trend, we are extending the ARMA model utility with Seasonal aspect through SARIMAX API. Similar to ARIMA API, we have order sequence that inputs $(p, d, q)$ whereas in SARIMAX along with order, seasonal sequence $s$ with $(P, D, Q, s)$ are fed in.

from statsmodels.tsa.statespace.sarimax import SARIMAX

def sarima_util(model_name, model_config, seasonal_order, exogenous=False, enforce_stationarity=False):

    model_output = {}
    for key in ticker_dict.keys():
        print(f"Training {key}")
        model_output[key] = {}
        exog = None
        exog_test = None
        if(exogenous):
            keys = ticker_dict.copy()
            del keys["P&G"]
            exog_keys = keys.keys()
            exog = df_train[exog_keys]
            exog_test = df_test[PREDICTION_START_DATE:PREDICTION_END_DATE][exog_keys]

        fit_model = None
        predictions_df = None
        try:
            model = SARIMAX(df_train[key], order=model_config, seasonal_order=seasonal_order, exog=exog, enforce_stationarity=enforce_stationarity)
            fit_model = model.fit()
            predictions_df = fit_model.predict(start=min(df_test.index), end=max(df_test.index), exog=exog_test)
            model_output[key]["isFit"] = True
        except Exception as e:
            print("Exception Occurred, while training {key} : ", e.__class__)
            print(e)

            model_output[key]["isFit"] = False

        model_output[key]["model"] = fit_model
        model_output[key]["predictions"] = predictions_df

    return model_output

SARMA

# Freeze
sarma_model = sarima_util("SARMA", (1, 0, 1), seasonal_order=(1, 0, 1, 5))
plt_predictions(df_test[PREDICTION_START_DATE:PREDICTION_END_DATE], sarma_model, "Seasonal Auto Regressive Moving Averages(MA)")

Training Unilever


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "


Training P&G
Training Nestle
Training Diageo

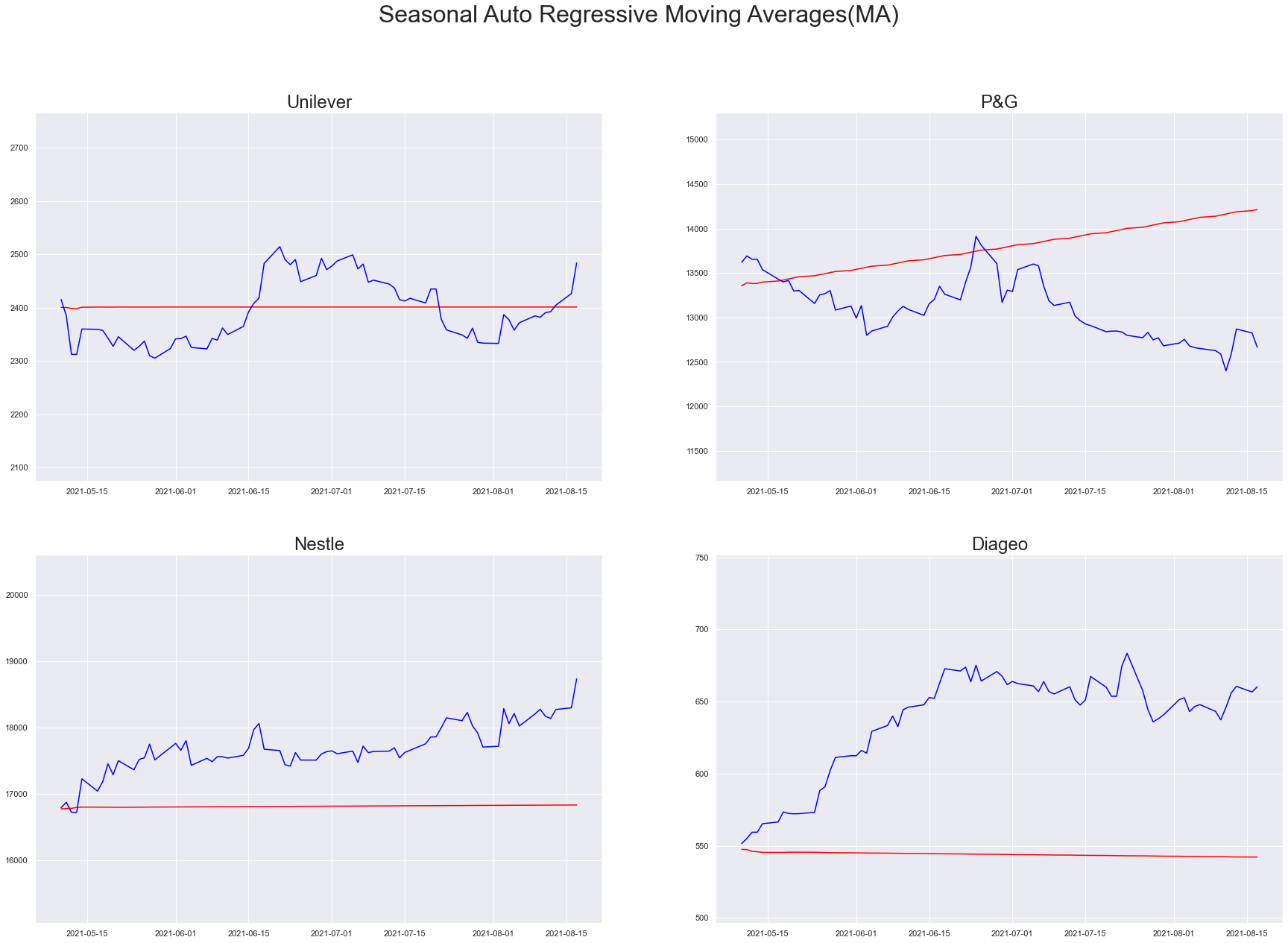
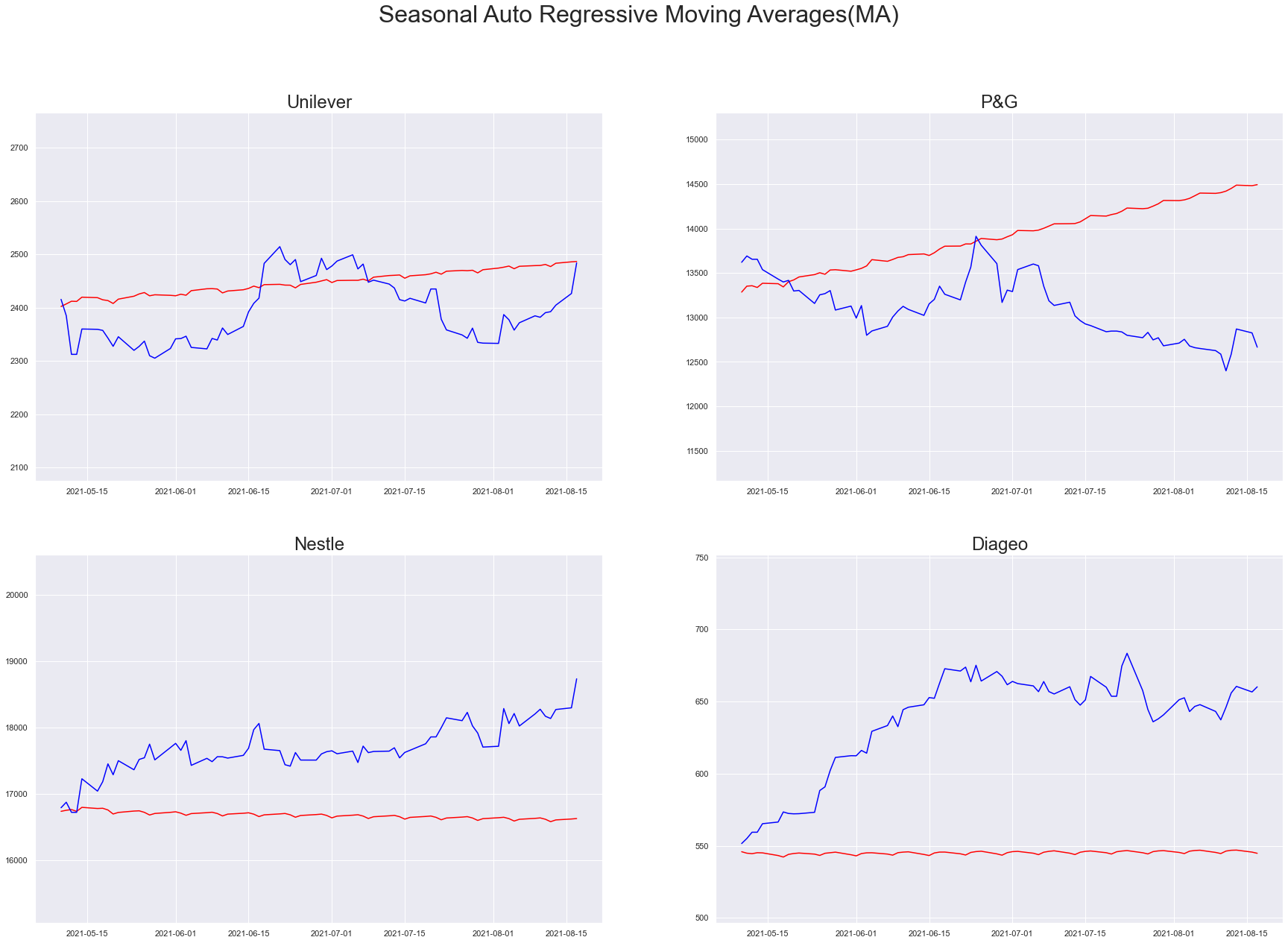
SARIMA

As we add more and more information to the modeling scheme, our prediction plots are showing significant change in the predictability. It is quite evident in SARIMA, tweaking the order and seasonal order hyperparameter is the key activity for convergence.

sarma_model = sarima_util("SARMA", (3, 1, 4), seasonal_order=(3, 1, 2, 5))
plt_predictions(df_test[PREDICTION_START_DATE:PREDICTION_END_DATE], sarma_model, "Seasonal Auto Regressive Moving Averages(MA)")

Training Unilever


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "


Training P&G


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "


Training Nestle


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "


Training Diageo


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "

Exogenous Model(X)

Exogenous models learn patterns from the external data, In this study we feed Unilever, Nestle and Diageo data as exogenous ones to predict P&G’s outcomes. In this section we shall compare the predictability of various combinations of model schemes.

def exogenous_util(ticker, order, seasonal_order=None, enforce_stationarity=False):
    model_output = {}
    print(f"Training {ticker}")
    model_output = {}


    keys = ticker_dict.copy()
    del keys["P&G"]
    exog_keys = keys.keys()
    exog = df_train[exog_keys]
    exog_test = df_test[PREDICTION_START_DATE:PREDICTION_END_DATE][exog_keys]

    fit_model = None
    predictions_df = None
    try:
        model = SARIMAX(df_train[ticker], order=order, seasonal_order=seasonal_order, exog=exog, enforce_stationarity=enforce_stationarity)
        fit_model = model.fit()
        predictions_df = fit_model.predict(start=min(df_test.index), end=max(df_test.index), exog=exog_test)
        model_output["isFit"] = True
    except Exception as e:
        print("Exception Occurred, while training {key} : ", e.__class__)
        print(e)

        model_output["isFit"] = False

    model_output["model"] = fit_model
    model_output["predictions"] = predictions_df

    return model_output

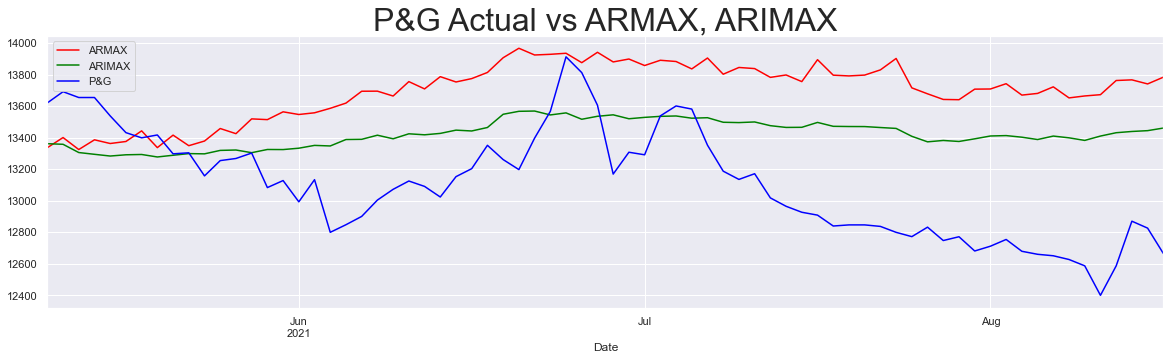
ARIMAX

We are also enforcing stationarity in these models to notice how better the models are converging as we add more and more information.

armax_models = exogenous_util("P&G", (3, 0, 4), enforce_stationarity=True)
arimax_models = exogenous_util("P&G", (3, 1, 4), enforce_stationarity=True)

Training P&G


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "


Training P&G


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "

plt.figure(figsize=(20, 5))
armax_models["predictions"].plot(color="red", label="ARMAX")
arimax_models["predictions"].plot(color="green", label="ARIMAX")
df_test["P&G"].plot(color="blue")
plt.legend()
plt.title("P&G Actual vs ARMAX, ARIMAX", size=32)
plt.show()
# plt_predictions(df_test[PREDICTION_START_DATE:PREDICTION_END_DATE], armax_models, "Auto Regressive Moving Averages(MA)")

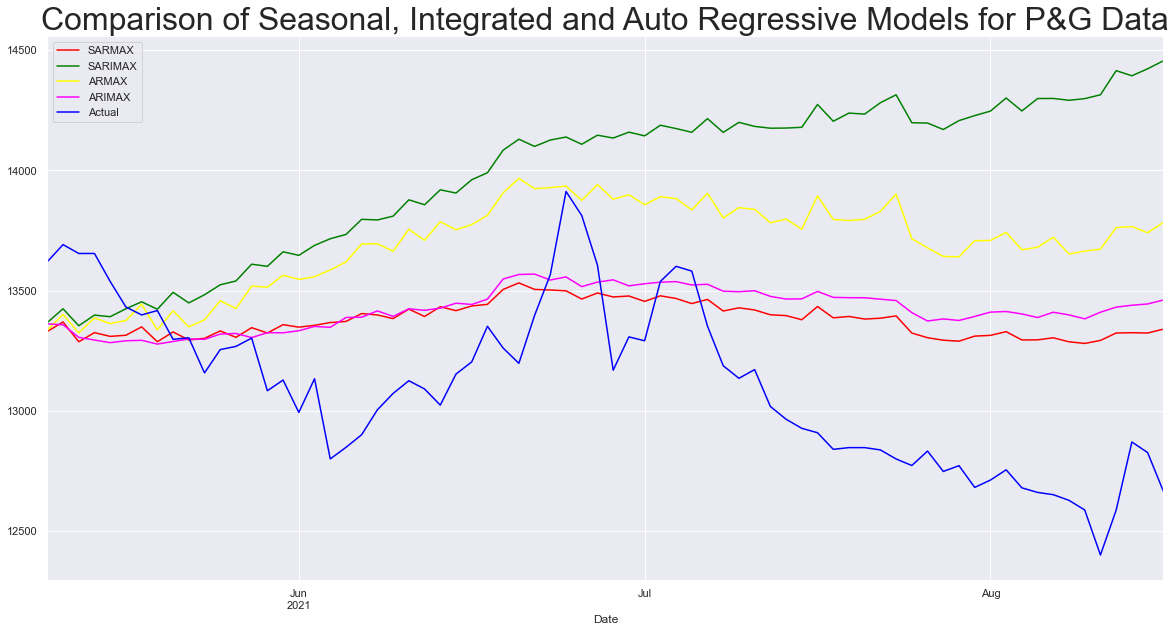
SARIMAX

# Freeze
sarmax_model = exogenous_util("P&G", (3, 0, 4), seasonal_order=(3, 0, 2, 5), enforce_stationarity=True)
sarimax_model = exogenous_util("P&G", (3, 1, 4), seasonal_order=(3, 1, 2, 5), enforce_stationarity=True)
print(sarmax_model.keys())

Training P&G


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "


Training P&G


/Users/shankar/dev/tools/anaconda3/envs/od/lib/python3.8/site-packages/statsmodels/base/model.py:566: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "


dict_keys(['isFit', 'model', 'predictions'])

plt.figure(figsize=(20, 10))
sarmax_model["predictions"].plot(color="red", label="SARMAX")
sarimax_model["predictions"].plot(color="green", label="SARIMAX")
armax_models["predictions"].plot(color="yellow", label="ARMAX")
arimax_models["predictions"].plot(color="magenta", label="ARIMAX")
df_test["P&G"].plot(color="blue", label="Actual")
plt.legend()
plt.title("Comparison of Seasonal, Integrated and Auto Regressive Models for P&G Data", size=32)

plt.show()

Conclusion

In this post we studied how to use statsmodel package by explore 8 different model types. We also visualize the outcomes graphically, the models we studied from Auto Regressive(AR) to Seasonal Auto Regressive Integrated Moving Average with Exogenous Data(SARIMAX) equip us with understanding and practical implementation of Univariate Time Series analysis and forecasting.

References

• Tutorial of Statsmodel Package
• Hidden Markov Model: Simple Definition & Overview
• Moving-average model from Wikipedia
• ARMA model
• Stationarity & Differencing: Definition, Examples, Types
• Stationarity from Engineering Statistics Handbook
• Extending the ARMA model: Seasonality and trend by Edward Lonides, 2016